Third Midterm-Practice Test

Leave a comment Go to comments

You know the drill.

Find the volume of the solid that lies under the plane $3x+2y+z=12$ and above the rectangle $R=\big\{ (x,y) : 0 \leq x \leq 1, -2 \leq y \leq 3 \big\}.$
Find the volume of the solid enclosed by the paraboloid $z=2+x^2+(y-2)^2$ and the planes $z=1, x=1, x=-1, y=0$ and $y=4.$
For the integral $\int_0^1 \int_{4x}^4 f(x,y)\, dy\, dx$ , sketch the region of integration and change the order of integration.
Find the volume of the solid enclosed by the parabolic cylinder $y=x^2$ and the planes $z=3y, z=2+y.$
Use a double integral to find the are of the region inside the cardioid $r=1+\cos \theta$ and outside the circle $r=3\cos\theta.$
Use polar coordinates to combine the sum below into one double integral, and evaluate it.
$\displaystyle{ \int_{1/\sqrt{2}}^1 \int_{\sqrt{1-x^2}}^x xy\, dy\, dx + \int_1^{\sqrt{2}} \int_0^x xy\, dy\, dx + \int_{\sqrt{2}}^2 \int_0^{\sqrt{4-x^2}} xy\, dy\, dx}.$
A swimming pool is circular with a 40-ft diameter. The depth is constant along east-west lines and increases linearly from 2 ft at the south end to 7 ft at the north end. Find the volume of water in the pool.
The boundary of a lamina consists of the semicircles $y = \sqrt{1-x^2}$ and $y=\sqrt{4-x^2}$ together with the portions of the $x$ –axis that join them. Find the center of mass of the lamina if the density at any point is proportional to its distance from the origin.
Express the volume of the wedge in the first octant that is cut from the cylinder $y^2+z^2=1$ by the planes $y=x$ and $x=1$ as a triple integral.
Evaluate the triple integral $\iiint_E z\, dV$ where $E$ is bounded by the cylinder $y^2+x^2=9$ and the planes $x=0, y=3x$ and $z=8$ in the first octant.
Identify the surface with equation in cylindrical coordinates given by $z=4-r^2.$
Evaluate $\iiint_E e^{\sqrt{x^2+y^2+z^2}}\, dV,$ where $E$ is enclosed by the sphere $x^2+y^2+z^2=9$ in the first octant.
Find the volume of the part of the ball $\rho\leq a$ that lies between the cones $\phi = \pi/6$ and $\phi=\pi/3.$
Find the Jacobian of the transformation $x=v+w^2, y=w+u^2, z=u+v^2.$
By using an appropriate change of variables, evaluate the integral $\iint_R \frac{x-2y}{3x-y}\, dA,$ where $R$ is the parallelogram enclosed by the lines $x-2y=0, x-2y=4, 3x-y=1$ and $3x-y=8.$

Comments (17) Leave a comment

Bobby F

November 11, 2011 at 9:34 pm

Reply

For number 2, I want to see if I’ve set it up correctly (these ones confuse me somewhat).

I called u1 -> z = 1 and u2 -> z = 2 + x^2 + (y – 2)^2

So I set up the problem to be where you first take the integral of 1 dz from u1 to u2, and then integrate that resulting function over the domain D. Where D = {(x,y) : -1 <= x <= 1 ; 0 <= y <= 4}

Is that how you set up this problem?
- Francisco Blanco-Silva
  
  November 12, 2011 at 7:45 am
  
  Reply
  
  yes
Bobby F

November 11, 2011 at 10:18 pm

Reply

Wanna check my setup again.

For number 4 I got u1 -> z = 3y and u2 -> z = 2 + y

Then I set up the problem to be the integral of 1 dz from u1 to u2, and then integrate that resulting function over the domain D. Where D = {(x,y): 0 <= y <= 1; -sqrt(y) <= x <= sqrt(y)}

Tell me what you think. Thanks
- Francisco Blanco-Silva
  
  November 12, 2011 at 8:15 pm
  
  Reply
  
  That’s pretty good! Number 4 is a tough problem to visualize, yet you got the right equations. Would you care to explain how you obtained them to the rest of the class (here)?
- Bobby F
  November 13, 2011 at 10:16 am
  
  Reply
  Sure.
  Well, as you said, it’s very hard to visualize, and that’s why I wanted to check it.
  
  The first thing I noticed was that the equation $y = x^2$ is a parabolic cylinder which is just your classic $y = x^2$ at every point $z$ . So it runs parallel to the $z$ axis with its “spine” touching the $z$ axis.
  
  Then you have the two planes $z = 3y$ and $z = 2 + y.$ These are two flat planes that are parallel to the $x$ axis. You know this b/c $x$ is not in the equation. Now remember that just b/c they are parallel to the $x$ axis, doesn’t mean they are not tilted (b/c they are). They are tilted and they intersect. You can do a quick check of this and say that $3y = 2 + y$ which means that they intersect at $y = 1$ and $z = 3.$
  
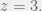
  This is where it gets tricky to visualize. Here’s what we can say about the three surfaces…
  
  We have a simple parabolic cylinder that runs with its spine up the $z$ axis.
  
  We have two planes that will slice through that cylinder.
  
  The planes are parallel to the $x$ -axis but not parallel to each other, so they will intersect.
  
  Since the intersection occurs when $y$ and $z$ are both positive the intersection is somewhere “inside” the parabolic cylinder.
  
  This describes our enclosed solid area. Now we just have to figure out what the bounds of $x, y,$ and $z$ are. Since the parabolic cylinder is parallel to the $z$ -axis it will NOT be our top or bottom surface ( $u1$ and $u2$ ). That means our two planes must be $u1$ and $u2$ (the $z$ boundaries). The domain of $x$ is pretty easy. Our parabolic cylinder is $y = x^2.$ That means that $x$ goes from $-\sqrt{y}$ to $\sqrt{y}$ (just solve for $x$ ). 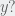So what is the domain of $y?$ Well the lowest $y$ will be is zero, But what about the highest it can be? Remember how the two planes intersect “inside” the mouth of the parabolic cylinder? 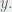That intersection is the max value of $y.$ We found that to be 1 up above. So that gives us
  
  $\big\{ (x,y,z) : 0 \leq y \leq 1, -\sqrt{y} \leq x \leq \sqrt{y}, 3y \leq z \leq 2 + y \big\}$
  
  Solving it is easy. We’re just finding the volume. So we take the integral of the function 1 with respect to $z$ and then integrate that resulting function on the domain $x$ and $y.$
  
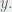
  Sorry for the long explanation. I tried to be as descriptive as possible since it’s so hard to visualize.
  - Paul Hewitt
    
    November 16, 2011 at 6:24 pm
    
    Reply
    
    Shouldn’t the bounds of Y be: x^2 <= y <= 1? Since your cylinder's spine is on the Z axis.
    - Francisco Blanco-Silva
      
      November 16, 2011 at 7:24 pm
      
      Reply
      
      Bobby’s description is good, but not the only one. Another possible description (using your bounds) for the region is as follows:
      
      $\big\{ (x,y,z) : -1 \leq x \leq 1, x^2 \leq y \leq 1, 3y \leq z \leq 2+y \big\}$
Bobby F

November 13, 2011 at 8:55 pm

Reply

For number 6…

Does anyone have any clue where to start?
Bobby Frankenberger

November 14, 2011 at 11:48 am

Reply

Number 10 is confusing me.

It doesn’t seem like there is an upper bound for the domain of z. Am I missing something?
- Francisco Blanco-Silva
  
  November 14, 2011 at 1:48 pm
  
  Reply
  
  There was a typo. Thanks for noticing! It is fixed now.
  - Paul
    
    November 15, 2011 at 12:28 am
    
    Reply
    
    This one had me screwed up too. I am glad it was just a typo and nothing more complicated.
Darya

November 14, 2011 at 12:26 pm

Reply

I noticed you did not assign homework from 15.7. Will there be questions from this section on the exam?
- Francisco Blanco-Silva
  
  November 14, 2011 at 1:40 pm
  
  Reply
  
  The problems are similar to those in 15.8. If you can do 15.8, then the ones in 15.7 should not be too much trouble. But yeah, there will be at least a question from that section.
Mitch G.

November 16, 2011 at 10:41 am

Reply

I have been working on problem number 5 and I know what to do, however I did something wrong in the setup because I got a negative number. First, I set these equations equal, since both are equal to r, and found that there are two points of intersection and they are (pi/3) and (5pi/3). From there, I created 2 double integrals, 1 to account for the area between these points of the cardioid, and the other to subtract the area covered by the circle between these two points.

For the cardioid, I set up a double integral with the following bounds:

0 < r < 1+cos(theta)
(pi/3) < theta < 5(pi/3)

And integrated 1 to find the area of the region. I then set up the double integral for the circle using r going from 0 to 3cos(theta) and the same bounds for theta. Doing this gave me a negative number and I'm not exactly sure why.
- Francisco Blanco-Silva
  
  November 16, 2011 at 12:00 pm
  
  Reply
  
  You have to be careful how to compute the angles of intersection, that’s all.
  
  To see why, using WolframAlpha, plot first $r=1+\cos\theta$ between $\pi/3$ and $5\pi/3$ . Note that this is exactly what we would expect. Now, plot $r=3\cos\theta$ between the same two angles: what do you observe?
  
  In Calc II we learned how to treat this appropriately: See example 3 in section 10.4 (page 652)
  - Paul Hewitt
    
    November 16, 2011 at 9:31 pm
    
    Reply
    
    Wouldn’t an easier approach be to just double the area that you get from doing the double integral between the two functions from pi/3 to pi?
    - Francisco Blanco-Silva
      
      November 16, 2011 at 11:54 pm
      
      Reply
      
      Definitely! But be careful: for the cardioid it is indeed from $\pi/3$ to $\pi$ . For the circle, it is a different set of angles.