Advanced Problem #18
Another fun problem, as requested by Qinfeng Li in MA598R: Measure Theory
Let
so that
too.
Show that
and
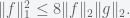
I got this problem by picking some strictly positive value and breaking the integral
as follows:
Let us examine now the factors and
above:
We have thus proven that with
At this point, all you have to do is pick
(provided the denominator is not zero) and you are done.
34.000710
-81.034814
Comments (0)
Trackbacks (0)
Leave a comment
Trackback
We have moved!
On November 2014, I migrated this blog to blancosilva.github.io. Please update your bookmarks and RSS feeds accordingly.
In the news:
Recent Posts
- Migration
- Computational Geometry in Python
- Searching (again!?) for the SS Central America
- Jotto (5-letter Mastermind) in the NAO robot
- Robot stories
- Advanced Problem #18
- Book presentation at the USC Python Users Group
- Areas of Mathematics
- More on Lindenmayer Systems
- Some results related to the Feuerbach Point
- An Automatic Geometric Proof
- Sympy should suffice
- A nice application of Fatou’s Lemma
- Have a child, plant a tree, write a book
- Project Euler with Julia
- Seked
- Nezumi San
- Ruthless Thieves Stealing a Roll of Cloth
- Which one is the fake?
- Stones, balances, matrices
- Buy my book!
- Trigonometry
- Naïve Bayes
- Math still not the answer
- Sometimes Math is not the answer
- What if?
- Edge detection: The Convolution Approach
- OpArt
- So you want to be an Applied Mathematician
- Smallest Groups with Two Eyes
- The ultimate metapuzzle
- Where are the powers of two?
- Geolocation
- Boundary operators
- The Cantor Pairing Function
- El País’ weekly challenge
- Math Genealogy Project
- Basic Statistics in sage
- A Homework on the Web System
- Apollonian gaskets and circle inversion fractals
- Toying with basic fractals
- Unusual dice
- Wavelets in sage
- Edge detection: The Scale Space Theory
- Bertrand Paradox
- Voronoi mosaics
- Image Processing with numpy, scipy and matplotlibs in sage
- Super-Resolution Micrograph Reconstruction by Nonlocal-Means Applied to HAADF-STEM
- The Nonlocal-means Algorithm
- The hunt for a Bellman Function.
- Presentation: Hilbert Transform Pairs of Wavelets
- Presentation: The Dual-Tree Complex Wavelet Transform
- Presentation: Curvelets and Approximation Theory
- Poster: Curvelets vs. Wavelets (Mathematical Models of Natural Images)
- Wavelet Coefficients
- Modeling the Impact of Ebola and Bushmeat Hunting on Western Lowland Gorillas
- Triangulations
- Mechanical Geometry Theorem Proving
Pages
- About me
- Books
- Curriculum Vitae
- Research
- Teaching
- Mathematical Imaging
- Introduction to the Theory of Distributions
- An Introduction to Algebraic Topology
- The Basic Practice of Statistics
- MA598R: Measure Theory
- MA122—Fall 2014
- MA141—Fall 2014
- MA142—Summer II 2012
- MA241—Spring 2014
- MA242—Fall 2013
- Past Sections
- MA122—Spring 2012
- MA122—Spring 2013
- Lesson Plan—section 007
- Lesson Plan—section 008
- Review for First part (section 007)
- Review for First part (section 008)
- Review for Second part (section 007)
- Review for Third part (section 007)
- Review for the Second part (section 008)
- Review for the Fourth part (section 007)
- Review for Third and Fourth parts (section 008)
- MA122—Fall 2013
- MA141—Spring 2010
- MA141—Fall 2012
- MA141—Spring 2013
- MA141—Fall 2013
- MA141—Spring 2014
- MA141—Summer 2014
- MA142—Fall 2011
- MA142—Spring 2012
- MA241—Fall 2011
- MA241—Fall 2012
- MA241—Spring 2013
- MA242—Fall 2012
- MA242—Spring 2012
- First Midterm Practice Test
- Second Midterm-Practice Test
- Third Midterm—Practice Test
- Review for the fourth part of the course
- Blake Rollins’ code in Java
- Ronen Rappaport’s project: messing with strings
- Sam Somani’s project: Understanding Black-Scholes
- Christina Papadimitriou’s project: Diffusion and Reaction in Catalysts
- Problem Solving
- Borsuk-Ulam and Fixed Point Theorems
- The Cantor Set
- The Jordan Curve Theorem
- My oldest plays the piano!
- How many hands did Ernie shake?
- A geometric fallacy
- What is the next number?
- Remainders
- Probability and Divisibility by 11
- Convex triangle-square polygons
- Thieves!
- Metapuzzles
- What day of the week?
- Exact Expression
- Chess puzzles
- Points on a plane
- Sequence of right triangles
- Sums of terms from Fibonacci
- Alleys
- Arithmetic Expressions
- Three circles
- Pick a point
- Bertrand Paradox
- Unusual dice
- El País’ weekly challenge
- Project Euler with Julia
- LaTeX
Categories
aldebaran
algebra
algorithm
analysis
applied mathematics
approximation theory
books
calculus
catalyst
chemical engineering
circumcenter
coding
combinatorics
computational geometry
curvelets
data mining
Delaunay
denoising
differential geometry
edge detection
engineering
Euclidean geometry
fractal
functional analysis
geometry
harmonic analysis
history of math
image
image processing
imdb
Japan
L-system
LaTeX
latitude
Lindenmayer system
linear algebra
longitude
mathematical imaging
mathematics
matplotlibs
Measure Theory
metacritic
movie critics
movies
nonlocal means
numerical analysis
numpy
oxide
pattern recognition
physics
probability
programming
puzzles
python
sage
scanning transmission electron microscopy
scientific computing
scipy
segmentation
signal processing
statistics
stats
STEM
super-resolution
tex
tikz
tomography
topology
triangle
triangulation
trigonometry
Voronoi
voronoi diagram
wavelets
weights
Archives
- November 2014
- September 2014
- August 2014
- July 2014
- June 2014
- March 2014
- December 2013
- October 2013
- September 2013
- July 2013
- June 2013
- April 2013
- January 2013
- December 2012
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- November 2011
- September 2011
- August 2011
- June 2011
- May 2011
- April 2011
- February 2011
- January 2011
- December 2010
- May 2010
- April 2010
- September 2008
- September 2007
- August 2007
Join 64 other subscribers
 Math updates on arXiv.org
Math updates on arXiv.org
- On the image of the total power operation for Burnside rings
- A note on hidden classes in spinor classification
- Modularity of certain products of the Rogers-Ramanujan continued fraction
- Complex Analytic Structure of Stationary Flows of an Ideal Incompressible Fluid
- Learning the local density of states of a bilayer moir\'e material in one dimension
- Hypergeometric Distribution Revisited: Tail Inequalities, Confidence Bounds and Sample Sizes
- Positive formula for the product of conjugacy classes on the unitary group
- Neural Estimation Of Entropic Optimal Transport
- Some Homological Conjectures Over Idealization Rings
- On kernels of homological representations of mapping class groups
 sagemath
sagemath
- An error has occurred; the feed is probably down. Try again later.



