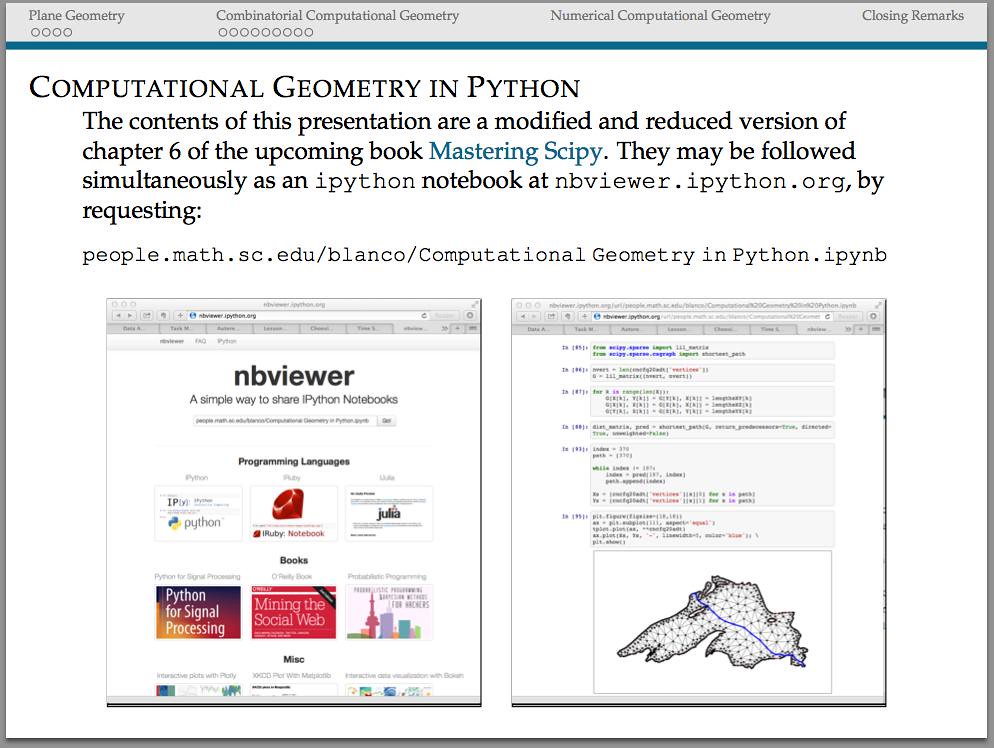
Archive
An Automatic Geometric Proof
We are familiar with that result that states that, on any given triangle, the circumcenter, centroid and orthocenter are always collinear. I would like to illustrate how to use Gröbner bases theory to prove that the incenter also belongs in the previous line, provided the triangle is isosceles.
We start, as usual, indicating that this property is independent of shifts, rotations or dilations, and therefore we may assume that the isosceles triangle has one vertex at , another vertex at
and the third vertex at
for some value
In that case, we will need to work on the polynomial ring
since we need the parameter
free, the variables
and
are used to input the conditions for the circumcenter of the triangle, the variables
and
for centroid, and the variables
and
for the incenter (note that we do not need to use the orthocenter in this case).
We may obtain all six conditions by using sympy, as follows:
>>> import sympy
>>> from sympy import *
>>> A=Point(0,0)
>>> B=Point(1,0)
>>> s=symbols("s",real=True,positive=True)
>>> C=Point(1/2.,s)
>>> T=Triangle(A,B,C)
>>> T.circumcenter
Point(1/2, (4*s**2 - 1)/(8*s))
>>> T.centroid
Point(1/2, s/3)
>>> T.incenter
Point(1/2, s/(sqrt(4*s**2 + 1) + 1))
This translates into the following polynomials
The hypothesis polynomial comes simply from asking whether the slope of the line through two of those centers is the same as the slope of the line through another choice of two centers; we could use then, for example, It only remains to compute the Gröbner basis of the ideal
Let us use SageMath for this task:
sage: R.<s,x1,x2,x3,y1,y2,y3,z>=PolynomialRing(QQ,8,order='lex') sage: h=[2*x1-1,8*r*y1-4*r**2+1,2*x2-1,3*y2-r,2*x3-1,(4*r*y3+1)**2-4*r**2-1] sage: g=(x2-x1)*(y3-y1)-(x3-x1)*(y2-y1) sage: I=R.ideal(1-z*g,*h) sage: I.groebner_basis() [1]
This proves the result.
Sympy should suffice
I have just received a copy of Instant SymPy Starter, by Ronan Lamy—a no-nonsense guide to the main properties of SymPy, the Python library for symbolic mathematics. This short monograph packs everything you should need, with neat examples included, in about 50 pages. Well-worth its money.
To celebrate, I would like to pose a few coding challenges on the use of this library, based on a fun geometric puzzle from cut-the-knot: Rhombus in Circles
Segments
and
are equal. Lines
and
intersect at
Form four circumcircles:
Prove that the circumcenters
form a rhombus, with
Note that if this construction works, it must do so independently of translations, rotations and dilations. We may then assume that is the origin, that the segments have length one,
and that for some parameters
it is
We let SymPy take care of the computation of circumcenters:
import sympy
from sympy import *
# Point definitions
M=Point(0,0)
A=Point(2,0)
B=Point(1,0)
a,theta=symbols('a,theta',real=True,positive=True)
C=Point((a+1)*cos(theta),(a+1)*sin(theta))
D=Point(a*cos(theta),a*sin(theta))
#Circumcenters
E=Triangle(A,C,M).circumcenter
F=Triangle(A,D,M).circumcenter
G=Triangle(B,D,M).circumcenter
H=Triangle(B,C,M).circumcenter
Finding that the alternate angles are equal in the quadrilateral is pretty straightforward:
In [11]: P=Polygon(E,F,G,H) In [12]: P.angles[E]==P.angles[G] Out[12]: True In [13]: P.angles[F]==P.angles[H] Out[13]: True
To prove it a rhombus, the two sides that coincide on each angle must be equal. This presents us with the first challenge: Note for example that if we naively ask SymPy whether the triangle is equilateral, we get a False statement:
In [14]: Triangle(E,F,G).is_equilateral() Out[14]: False In [15]: F.distance(E) Out[15]: Abs((a/2 - cos(theta))/sin(theta) - (a - 2*cos(theta) + 1)/(2*sin(theta))) In [16]: F.distance(G) Out[16]: sqrt(((a/2 - cos(theta))/sin(theta) - (a - cos(theta))/(2*sin(theta)))**2 + 1/4)
Part of the reason is that we have not indicated anywhere that the parameter theta is to be strictly bounded above by (we did indicate that it must be strictly positive). The other reason is that SymPy does not handle identities well, unless the expressions to be evaluated are perfectly simplified. For example, if we trust the routines of simplification of trigonometric expressions alone, we will not be able to resolve this problem with this technique:
In [17]: trigsimp(F.distance(E)-F.distance(G),deep=True)==0 Out[17]: False
Finding that with SymPy is not that easy either. This is the second challenge.
How would the reader resolve this situation?