Archive
Where are the powers of two?
The following construction gives an interesting pairing map between the positive integers and the lattice of integer-valued points in the plane:
- Place
at the origin.
- For each level
populate the
points of the plane on the square with vertices
starting from
at the position
and going counter-clockwise.
After pairing enough positive integers on the lattice, pay attention to the powers of two: they all seem to be located on the same two horizontal lines: and
Is this statement true?
Geolocation
Recall the First Spherical Law of Cosines:
Given a unit sphere, a spherical triangle on the surface of the sphere is defined by the great circles connecting three points
,
, and
on the sphere. If the lengths of these three sides are
(from
to
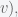
(from
to
and
(from
to
and the angle of the corner opposite
is
then
In any decent device and for most computer languages, this formula should give well-conditioned results down to distances as small as around three feet, and thus can be used to compute an accurate geodetic distance between two given points in the surface of the Earth (well, ok, assuming the Earth is a perfect sphere). The geodetic form of the law of cosines is rearranged from the canonical one so that the latitude can be used directly, rather than the colatitude, and reads as follows: Given points and
with positions
and
respectively, the distance
between the two points is given by the following formula.
where is the radius of the Earth in miles (well, ok, the average radius of the Earth…)
A nice application of this formula can be used for geolocation purposes, and I recently had the pleasure to assist a software company (thumb-mobile.com) to write such functionality for one of their clients.
 |
 |
 |
Go to www.lizardsthicket.com in your mobile device, and click on “Find a Location.” This fires up the location services of your browser. When you accept, your latitude and longitude are tracked. After a fast, reliable and resource-efficient algorithm, the page offers the location of the restaurant from the Lizard’s chain that is closest to you. Simple, right?





