Apollonian gaskets and circle inversion fractals

Recall the definition of an iterated function system (IFS), and how on occasion, their attractors are fractal sets. What happens when we allow more general functions instead of mere affine maps?

The key to the design of this amazing fractal is in the notion of limit sets of circle inversions.

Toying with basic fractals

I will skip all the mathematical theory behind Fractals (dimensions, measures, etc) to focus directly into the description and implementation of some of the most basic examples. In this post, I will cover the ideas behind three classical techniques:

• Iterated function systems
• Membership tests
• Lindenmayer systems

Unusual dice

I heard of this problem from Justin James in his TechRepublic post My First IronRuby Application. He tried this fun problem as a toy example to brush up his skills in ruby:

Roll simultaneously a hundred 100-sided dice, and add the resulting values. The set of possible outcomes is, of course, Note that there is only one way to obtain the outcome 100—all dice showing a 1. There is also only one way to obtain the outcome 10000—all dice showing 100. For the outcome 101, there are exactly 100 different ways to obtain it: all dice except one show a 1, and one die shows a 2. The follow-up question is:

Write a (fast) script that computes the different ways in which we can obtain each of the possible outcomes.

Read more…

Wavelets in sage

There are no native wavelet packages in sage. But there is a great module in python that contains, among other things, forward and inverse discrete wavelet transforms (for one and two dimensions). It comes bundled with seventy-six wavelet filters, and allows support to build your own! The name is PyWavelets, written by Tariq Rashid, and can be retrieved from pypi.python.org/pypi/PyWavelets. In order to install it in sage, take the following steps:

Read more…

Edge detection: The Scale Space Theory

Consider an image as a bounded function with no smoothness or structure assumptions a priori. Most relevant information of a given image is contained in the contours of the mapped objects: Think for example of a bright object against a dark background—the area where these two meet presents a curve where the intensity varies strongly. This is what we refer to as an “edge.”

Initially, we may consider the process of detection of an edge by the simple computation of the gradient This gradient should have a large intensity and a direction which indicates the perpendicular to the curve. It therefore looks sound to simply compute the gradient of and choose the points where these values are large. This conclusion is a bit unrealistic for two reasons:

1. The points where the gradient is larger than a given threshold are open sets, and thus don’t have the structure of curves.
2. Large gradient may arise in certain locations of the image due to tiny oscillations or noise, but completely unrelated to the objects being mapped. As a matter of fact, there is no reason to assume the existence or computability of any gradient at all in a given digital image.

Read more…

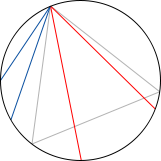
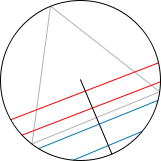
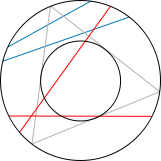
Bertrand Paradox

Classically, we define the probability of an event as the ratio of the favorable cases, over the number of all possible cases. Of course, these possible cases need to be all equally likely. This works great for discrete settings, like dice rolls, card games, etc. But when facing non-discrete cases, this definition needs to be revised, as the following example shows:

Consider an equilateral triangle inscribed in a circle. Suppose a chord of the circle is chosen at random. What is the probability that the chord is longer than a side of the triangle?

First example	Second example	Third example

Read more…

Voronoi mosaics

While looking for ideas to implement voronoi in sage, I stumbled upon a beautiful paper written by a group of japanese computer graphic professionals from the universities of Hokkaido and Tokyo: A Method for Creating Mosaic Images Using Voronoi Diagrams. The first step of their algorithm is simple yet brilliant: Start with any given image, and superimpose an hexagonal tiling of the plane. By a clever approximation scheme, modify the tiling to become a voronoi diagram that adaptively minimizes some approximation error. As a consequence, the resulting voronoi diagram is somehow adapted to the desired contours of the original image.

(Fig. 1)	(Fig. 2)	(Fig. 3)	(Fig. 4)

In a second step, they manually adjust the Voronoi image interactively by moving, adding, or deleting sites. They also take the liberty of adding visual effects by hand: emphasizing the outlines and color variations in each Voronoi region, so they look like actual pieces of stained glass (Fig. 4).