Bertrand Paradox

Classically, we define the probability of an event as the ratio of the favorable cases, over the number of all possible cases. Of course, these possible cases need to be all equally likely. This works great for discrete settings, like dice rolls, card games, etc. But when facing non-discrete cases, this definition needs to be revised, as the following example shows:

Consider an equilateral triangle inscribed in a circle. Suppose a chord of the circle is chosen at random. What is the probability that the chord is longer than a side of the triangle?

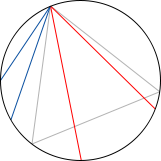
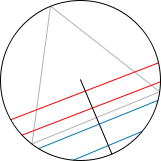
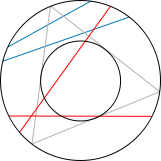
First example Second example Third example

Using the classical definition of probability, three different students attacked this problem independently, and found each a different result: In all three examples, assume the circle has radius 1.

Fix any point, say $P$ in the circle. Consider any random chord in the circle, by choosing any other point $Q$ on it. The number of possible cases is thus $(2\pi \times 1)^2 = 4\pi^2.$ Place one of the vertices of the equilateral triangle on $P$ , and notice that the circle gets partitioned in three arcs with equal length $(\tfrac{2\pi}{3}).$ Only if $Q$ belongs in the arc farthest to $P,$ we will have a chord longer than the side of the triangle. Therefore, the number of favorable cases is $2\pi \times \tfrac{2\pi}{3} = \tfrac{4\pi^2}{3}.$ Consequently, the probability we are looking for is $\tfrac{1}{3}.$
Choose any point $P$ on the circle, any point $Q_P$ on the radius $r_P=\overline{0P},$ and consider the chord formed from the perpendicular to $r_P$ by $Q_P.$ There are $2\pi \times 1 = 2\pi$ possible cases. Place the equilateral triangle so that one of the sides is perpendicular to $r_P,$ and notice that the number of favorable cases coincide with those chords where $Q_P$ is nearer the center of the circle than the point where the side of the triangle intersects the radius. A simple trigonometric computation tells us that the number of favorable cases is precisely $2\pi \times \tfrac{1}{2} = \pi,$ and thus the probability we are looking for is $\tfrac{1}{2}.$
Choose any point $P$ in the interior of the disk, and consider the only chord that has $P$ as a midpoint. There are $\pi \times 1^2 = \pi$ possible cases. The chord will be longer than the side of the triangle, only if the chosen point falls within a concentric circle of radius $\tfrac{1}{2}.$ The number of favorable cases is thus the area of this circle: $\pi \times \big( \tfrac{1}{2} \big)^2 = \tfrac{\pi}{4}.$ The probability we are looking for is in this case $\tfrac{1}{4}.$

The three methods are sound: why did we get different answers? Which student do you think got it “right”? Can you explain what the paradox is in this situation?

Comments (6) Trackbacks (0) Leave a comment Trackback

Ralph Howard

January 13, 2011 at 12:28 am

Reply

I started out my mathematical life doing integral geometry and at some point had to think hard about this question. The problem is that there are many measures on the space of chords and it depends on what you are doing as to which is the most “natural” to use. If one is constructing the chords by choosing two points on the circle and then connecting them, then the first solution is the most natural.

For those of use who have done integral geometry (= geometric probability) the natural way to look at this is as follows. Let Λ be the set of all lines in the plane. This has a measure, dL, discovered by the English mathematician Crofton in the late 1800’s such that for any bounded convex set D

∫ length ( D ∩ L ) dL = Area( D )

The set of chords in D is the set C := { D ∩ L : L ∈ Λ }. Note for any chord S ∈ C there
is a unique line Ŝ such that D ∩ Ŝ = S. The we give the space of chords, C, the measure induced from Λ, that is if A ⊆ C

measure of A in C = measure of { Ŝ : S ∈ A } in Λ

This gives a uniform method of defining a measure on the set of chords of a bounded convex sets that has some nice properties (such as translation and rotation invariance).

Then a calculation, that is not that hard, but long enough that I don’t want to type it, gives that using this measure on the space of chords to a circle that the probability is 1/2, that is the second of those above. But again it depends on the measure we choose on the spaces of chords what the correct answer is.
- blancosilva
  
  January 14, 2011 at 11:04 pm
  
  Reply
  
  Thanks for the comment, Ralph! I just came up with this nice follow-up question: For what values $0<p<1$ does it exist a measure $\mu_p$ on the space of chords so that "the probability that the chord is longer than a side of the triangle" is exactly $p$ ? My guess (and I think I know how to prove this) is that at least we should be able to find such $\mu_p$ for $\tfrac{1}{4} \leq p \leq \tfrac{1}{2}.$ We might be even able to find for all $0<p<1,$ although counter-intuitive. What do you think?
Thierry Zell

January 20, 2011 at 8:36 pm

Reply

I cannot believe that I reached this ripe old age without learning of this paradox! (More likely, I used to know about it and I forgot already.)

Along similar lines: what is the average number of real roots of a real polynomial of degree d? There are a few such results, the range I know is from root d to d/3. I don’t know all the details, but you pick coefficients independently and the key question is coefficients in which basis, with the larger bound obtained with the Chebyshev basis.
- blancosilva
  
  January 24, 2011 at 1:23 pm
  
  Reply
  
  That’s a nice one too! Care to elaborate? I will include it in a post.
Ralph Howard

January 23, 2011 at 10:40 pm

Reply

Here is a solution to your problem. For 0 < p < 1, choose a probability measure, μ, on the unit disk such that the disk of radius 1/2 has measure p. There are many such measures and we can even choose μ to be rotationally symmetric. If we then parametrize the chords by their midpoints, as in your third solution above, then the required probability is p.
- blancosilva
  
  January 23, 2011 at 10:18 pm
  
  Reply
  
  That’s a nice one! I guess that, although there is a modification on the way lengths and areas are measured, the length of any chord with midpoint in the inner circle will still have length larger than that on the side of the equilateral triangle.
  
  Do you think we can get it without altering the way we measure lengths and areas? I would like to keep the area of that circle as $\pi/4,$ as well as the lengths of segments from $\boldsymbol{x} = (x_1,x_2)$ to $\boldsymbol{y} = (y_1,y_2)$ to be $\sqrt{ (x_2-y_2)^2 + (x_1-y_1)^2}.$