Review for the Second part (section 008)
Note from the instructor: excellent practice test! There were three questions that I didn’t like (and I didn’t print them). The rest were pretty good, but I changed the coefficients of most of them, to prevent the use of answer keys.
- Find the derivative of
- The function
has a critical point at
Use the second derivative test to identify it as a local maximum or local minimum.
- Find the derivative of
- Find the value of the parameter
so that the function
has a critical point at
- Are the following examples power functions? If so, what are the corresponding values of
and
?
- Find and classify all the critical points of the function
- Find the domain, global maximum and global minimum of the function
- If you have 300 ft of fencing and wish to enclose a rectangular area up against a wall, what is the largest area that you can enclose? (note from the instructor: this is a really good problem)
- If the cost function is
find the marginal cost to produce the 200th unit and the average cost of producing 200 units.
- At a price of $8 per ticket, a musical theater group can fill every seat in the theater, which has a capacity of 2,500. For every additional dollar charged, the number of people buying tickets decreases by 50. What ticket price maximizes revenue? (note from the instructor: this is another really good problem!)
- A company estimates that the total revenue (in dollars) received from the sale of
items is
Calculate and interpret the marginal revenue when
Leave a comment
Blanco-Silva’s Books
Click on either image for more information
In the news:
Math updates on arXiv.org
- On the image of the total power operation for Burnside rings
- A note on hidden classes in spinor classification
- Modularity of certain products of the Rogers-Ramanujan continued fraction
- Complex Analytic Structure of Stationary Flows of an Ideal Incompressible Fluid
- Learning the local density of states of a bilayer moir\'e material in one dimension
- Hypergeometric Distribution Revisited: Tail Inequalities, Confidence Bounds and Sample Sizes
- Positive formula for the product of conjugacy classes on the unitary group
- Neural Estimation Of Entropic Optimal Transport
- Some Homological Conjectures Over Idealization Rings
- On kernels of homological representations of mapping class groups
sagemath
- An error has occurred; the feed is probably down. Try again later.
Francisco Blanco-Silva 
Can someone help me on #7 please….I don’t know how to get the locals without being given the intervals.
Thanks,
Brooke Balentine
When I asked him in class, Mr. Blanco-Silva said this one was much harder than any of the problems he’s written this year.
0 then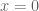 
Step 1: Rewrite as
Step 2:
Step 3:
Blanco-Silva also said that if it a global max/global min problem then the best option is to plug the function in your calculator and do TRACE and MAXIMUM
Do you know if the answer for both the max and min is 0?
He said there was only one critical point so I think that’s the only point he would be looking for but you can also trace min in the calculator
Is the domain all real numbers? I know to find domain, the denominator cannot equal 0 so I set 4+x^2=0 but then you get a negative 4 when you try to take the square root of both sides. What do you end up with as your domain?
How do I start problem 8?
Will
It’s an optimization problem. Start by finding the formula for the amount of fencing given, which is 2x+y=300. To find the max area that can be enclosed by this, take the derivative of the function and set it equal to zero, then solve for x.
Ah, sorry. I meant to add that you need to find the formula for area, x*y=area, then solve for y in the first function so you only have one variable. Then plug that into the area function, THEN start the optimization.
I have no clue how to do number 9, can anyone help?
c'(q) = 22$/unit ==> [101 + 22(200)]/ 200 ==> 4501/200 = 22.5 $/unit this is the instantaneous price per unit after 200 units are produced. therefore the cost of producing the 201st unit is 22.5 $
ok thanks, so 22 is the marginal cost which you got by taking the derivative of the function, and 22.5 is the average cost of producing 200 units?
Can someone help me with #6?
6.) first you have to find the derivative of the equation & remember to use the equation F(x)= u’ * v(x) + u(x) * v’. Then to solve for critical points you have to set the derivative to zero.
Can someone tell me how to know if a function is a power function again? (question 5)
For a power function, the general form is f(x)= kx^p where p is any real number and k is non-zero. So if the function fits this general form, then it should be power function (if I am correct).
Does anyone have the correct answer for #11? I think I’m doing it right, but I keep getting 0.3 as the answer. To calculate marginal revenue, you have to take the derivative of the total revenue function given and then solve that for when q= 10, right?
I got 0.3 as the answer too, the way I did it was I took the derivative and then divided it by the original equation.
600(q)^2/(4+200(q)^3), and just plug in 10 for q.
I got .3 also but that seems weird!
For problem 8 is there a formula we use to find the largest area or is it just by estimations and process of elimination?
For #8 I’m pretty sure the formula is Area= x(300-2x) aka f(x)=300x-2x^2 and I think for this problem you find the derivative which would be F'(x)=300-4x and solve for x. I’m not 100% that’s how you do it but I’m going to ask Blanco-Silva in class how to do it.
I know its a really easy question, but how do you do #8???
Step 1: find two functions to represent the perimeter and area of the enclosure. Let 2x+y=300 be the length of fencing and xy=area.
Step 2: Solve for a variable, whichever is easiest. Solving for y is: y=300-2x
Step 3: Plug that equation into the area one so you have a function with one variable: x(300-2x)=area simplified is 2x^2+300x=area
Step 4: Take the derivative of the function and set it equal to zero. Solve for x. This is the max area to be enclosed. It should be 75 sq/ft.
Is 75 the width of one side of the wall? or is that the area itself? I thought you might have to plug 75 back into the area equation to find the max area?
How do you solve #4?
You find the derivative, set it equal to zero and plug 3 into the x’s! Then solve for a
I keep getting 1/9 as a and it isn’t working when I plug it back in. Does anyone know the actual answer?
To find critical points, take the derivative of a function, set it equal to zero, and solve for the unknown variable (in this case it’s a, since x is given).
The derivative is found by using the product rule. It should come out to: 3e^ax + (3x)(ae^ax).
Next, plug 3 in for all the x’s in the function so a is the only unknown variable and set the function to zero: 3e^3a+9ae^3a = 0.
Using logarithmic rules we can simplify this to (3a+1)3e^3a = 0. You’re supposed to be able to find the zeroes from this. 3e^3a will never equal zero, so rule it out. Then solve 3a+1=0 for a, and that is the value. You can check by plugging the original function in a graph with your solution as a and searching for the value x=3.
For #5, can someone confirm the form of the power function? I know it’s when you can write it with k and r but I cannot find the form in my notes!!! Thanks!
just saw carson’s comment, nevermind!
Here’s the way Mr. Blanco-Silva worded power functions in our class notes: “We say that a function is a power function if it can be written in the form y=f(x)=kx^r for some real numbers k, and r.” Therefore, both ‘A’ and ‘B’ fit the description of a power function. Part A is pretty self explanatory, and for Part B- 47 can be written as 47x^0, where k=47 and r=0.
Wait so 47 is a power function!? I thought it wasn’t but I guess that makes sense if you can write it like that. X^0=1?
Anybody know how to do number 10?
What are the rules for power functions?
-Karlie Bennett
I asked earlier on here and the answer I was given was “For a power function, the general form is f(x)= kx^p where p is any real number and k is non-zero. So if the function fits this general form, then it should be power function”
just saw matt’s post, nevermind!
For number 8, what did you guys get for x and y?
See my post above, #26.
For number 1, would you take the ln to get the x^5 out of the exponent? If not, how would you do the problem?
It should be a product rule.
Can someone who made question #1 confirm the answer?? I got (20x^5)(e^(x^5))+4e(^x^5) after simplifying. I did a product rule with 4x as the u and e^x^5 as the v. Is that how you do it?
Carly, I made the first equation and that’s what I got too! But he changed the numbers for this equation so i had resolve it.
Thanks!
I understand how to calculate #11, but how do you interpret it?
Can anyone go through how to do question ten for me?
Its a guess and check kind of problem. At 8 dollars they can fill the 2500 seats making 20,000 dollars. Charging 9 dollars they can only fill 2450 seats because with every dollar additional you charge you loose 50 seats. But 9 * 2450 = 22050. Continue doing this until you reach the maximum you can make. You will know its the max because the next one you calculate, the profit will have gone down.
The answer is $11 with a profit of $25850
Does anyone know how to start number 10?
On #6, when I use the product rule to find the derivative I get (3x^2(1-x)^4)+((x^3) 4(1-x)^3). I know I need to set this to zero to solve for the critical points, but how would I do that with all the variables?
i know a lot of people have asked, but could someone please go over number ten?
Yeah I need help with Number 10 also