Archive
Searching (again!?) for the SS Central America

On Tuesday, September 8th 1857, the steamboat SS Central America left Havana at 9 AM for New York, carrying about 600 passengers and crew members. Inside of this vessel, there was stowed a very precious cargo: a set of manuscripts by John James Audubon, and three tons of gold bars and coins. The manuscripts documented an expedition through the yet uncharted southwestern United States and California, and contained 200 sketches and paintings of its wildlife. The gold, fruit of many years of prospecting and mining during the California Gold Rush, was meant to start anew the lives of many of the passengers aboard.
On the 9th, the vessel ran into a storm which developed into a hurricane. The steamboat endured four hard days at sea, and by Saturday morning the ship was doomed. The captain arranged to have women and children taken off to the brig Marine, which offered them assistance at about noon. In spite of the efforts of the remaining crew and passengers to save the ship, the inevitable happened at about 8 PM that same day. The wreck claimed the lives of 425 men, and carried the valuable cargo to the bottom of the sea.
It was not until late 1980s that technology allowed recovery of shipwrecks at deep sea. But no technology would be of any help without an accurate location of the site. In the following paragraphs we would like to illustrate the power of the scipy stack by performing a simple simulation, that ultimately creates a dataset of possible locations for the wreck of the SS Central America, and mines the data to attempt to pinpoint the most probable target.
We simulate several possible paths of the steamboat (say 10,000 randomly generated possibilities), between 7:00 AM on Saturday, and 13 hours later, at 8:00 pm on Sunday. At 7:00 AM on that Saturday the ship’s captain, William Herndon, took a celestial fix and verbally relayed the position to the schooner El Dorado. The fix was 31º25′ North, 77º10′ West. Because the ship was not operative at that point—no engine, no sails—, for the next thirteen hours its course was solely subjected to the effect of ocean current and winds. With enough information, it is possible to model the drift and leeway on different possible paths.
Geolocation
Recall the First Spherical Law of Cosines:
Given a unit sphere, a spherical triangle on the surface of the sphere is defined by the great circles connecting three points
,
, and
on the sphere. If the lengths of these three sides are
(from
to
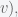
(from
to
and
(from
to
and the angle of the corner opposite
is
then
In any decent device and for most computer languages, this formula should give well-conditioned results down to distances as small as around three feet, and thus can be used to compute an accurate geodetic distance between two given points in the surface of the Earth (well, ok, assuming the Earth is a perfect sphere). The geodetic form of the law of cosines is rearranged from the canonical one so that the latitude can be used directly, rather than the colatitude, and reads as follows: Given points and
with positions
and
respectively, the distance
between the two points is given by the following formula.
where is the radius of the Earth in miles (well, ok, the average radius of the Earth…)
A nice application of this formula can be used for geolocation purposes, and I recently had the pleasure to assist a software company (thumb-mobile.com) to write such functionality for one of their clients.
 |
 |
 |
Go to www.lizardsthicket.com in your mobile device, and click on “Find a Location.” This fires up the location services of your browser. When you accept, your latitude and longitude are tracked. After a fast, reliable and resource-efficient algorithm, the page offers the location of the restaurant from the Lizard’s chain that is closest to you. Simple, right?



