Bertrand Paradox

Classically, we define the probability of an event as the ratio of the favorable cases, over the number of all possible cases. Of course, these possible cases need to be all equally likely. This works great for discrete settings, like dice rolls, card games, etc. But when facing non-discrete cases, this definition needs to be revised, as the following example shows:

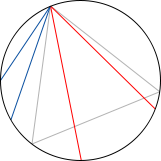
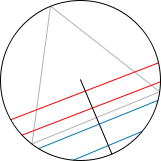
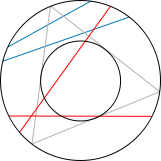
Consider an equilateral triangle inscribed in a circle. Suppose a chord of the circle is chosen at random. What is the probability that the chord is longer than a side of the triangle?

First example	Second example	Third example

Read more…