Second Midterm-Practice Test
You know the drill: Work these problems by yourself, and at some point start discussing the solutions with other students. In case of doubt, feel free to drop a comment and I will guide you with hints in the right direction. If you feel like it, drop also in the comments the answers that you obtained, so other students can check. Good luck!
- Plot a slope field for the following differential equations, and use it to indicate the stability or instability of their equilibria.
- The time rate of change of an alligator population
in a swamp is proportional to the square of
The swamp contained a dozen alligators in 1988, two dozen in 1998. When will there be four dozen alligators in the swamp? What happens thereafter?
- Suppose that the fish population
in a lake is attacked by a disease at time
with the result that the fish cease to reproduce and the death rate is thereafter proportional to
If there were initially 900 fish in the lake and 441 were left after 6 weeks, how long did it take all the fish in the lake to die?
- Consider an animal population
with constant death rate
(deaths per animal per month) and with birth rate
proportional to
Suppose that
and
When is
When does doomsday occur?
- The skid marks made by an automobile indicated that its brakes were fully applied for a distance of
before it came to a stop. The car in question is known to have a constant deceleration of
under these conditions. How fast (in
was the car traveling when the brakes were first applied?
- At noon a car starts from rest at a point A and proceeds with constant acceleration along a straight road toward point C, 35 miles away. If the constantly accelerated car arrives at C with a velocity of
at what time does it arrive at C?
- A ball is dropped from the top of a building
hight. How long does it take to reach the ground? With what speed does the ball strike the ground?
- Francisco bails out of an airplane at an altitude of
falls freely for 20 seconds, then opens his parachute. How long will it take him to reach the ground? Assume linear air resistance
taking
without the parachute and
with the parachute.

- Apply both Euler and Improved Euler methods to solving numerically the differential equation
with initial condition
in the interval
Use a time-step
Prepare a table showing four-decimal-place values of the approximate solution and the actual solution at the points
- [And the famous punch-line: If you are able to finalize in about 45 minutes, and are able to explain it to someone else, I consider that you have mastered this part of the course.] A tumor may be regarded as a population of multiplying cells. The “birth rate” of the cells in a tumor decreases exponentially with time, so that
where
and
are positive constants.
- [Find the differential equation] What is the corresponding population model?
- [Let’s find the values of
and
for a particular example] Suppose that at time
there are
cells and that
is then increasing at the rate of
cells per month. After 6 months the tumor has doubled (in size and in number of cells).
- [Use a slope field for this part, to support your claims] Find the limiting population of the tumor in the previous part.
- [Numerical Approximation] Use the improved Euler’s method to approximate the solution for this particular problem for the interval
Use a time step
For problem number 8, I don’t understand how to get the velocity and height. I have that so
so 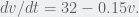 This is separable so
This is separable so 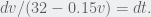 Integrating both sides gives
Integrating both sides gives 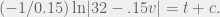 Using the fact that
Using the fact that  this equation becomes
this equation becomes 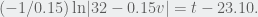 Solving for
Solving for  when
when  gives a ridiculously high number though. How am I supposed to go about finding the velocity and height?
gives a ridiculously high number though. How am I supposed to go about finding the velocity and height?
I used your last equation (which looks perfect), and plugged there. I obtained
there. I obtained  ft/s. It’s fast, I grant you that, but not too far fetched. What were you getting?
ft/s. It’s fast, I grant you that, but not too far fetched. What were you getting?
I got 202.71 ft/s for when From here I integrated the
From here I integrated the  equation to determine the final height before the parachute was opened. I have
equation to determine the final height before the parachute was opened. I have  Integrating, I got
Integrating, I got 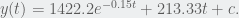 Using this to find
Using this to find 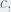 when
when  and
and  Using this equation to find
Using this equation to find  this yields a
this yields a 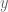 that is larger than the initial height, so I know that something got messed up. Could you help me with getting the correct
that is larger than the initial height, so I know that something got messed up. Could you help me with getting the correct 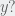
I used in another attempt, and got a better value for
in another attempt, and got a better value for  however this doesn’t make logical sense to me because this
however this doesn’t make logical sense to me because this 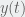 equation doesn’t match with proper integration.
equation doesn’t match with proper integration.
Y’all, notice that the choices of signs for the forces in Sam’s equation suggest that the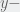 axis is directed downward (see the explanation in page 101 of the textbook). That is cool, but then you have to pick the correct signs and interpretation for your initial values and corresponding answers. My suggestion here is to use the convention that the positive branch of the
axis is directed downward (see the explanation in page 101 of the textbook). That is cool, but then you have to pick the correct signs and interpretation for your initial values and corresponding answers. My suggestion here is to use the convention that the positive branch of the 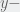 axis is pointing upwards, and then Newton Second Law for this case, after simplification of the masses, reads
axis is pointing upwards, and then Newton Second Law for this case, after simplification of the masses, reads  Go from there.
Go from there.
for velocity/acceleration models do we need to use the diff eqs. method to solve the problem or can we use prior knowledge from physics to solve them?
That’s a good question! You gotta show me that you have mastered the concepts taught in class, so it is best if you use differential equations. You can always rely on your expertise with Physics to make sure that your answers are correct!
For number 8 don’t you have to assume that the 32 ft/s^2 is negative?
See my reply to Sam and Sara above
For number 3, aren’t you supposed to interpret the situation as the rate at which the population is changing is equal to the negative death rate?
Yes
I’m not quite sure how to set up problem number 4 and I think I may be making similar mistakes in setting up the equations for the other population problems. For one, I haven’t seen a way to set up the typical logistic, explosion/extermination, or harvesting equations we saw in class, So I have been plugging in the birth and death rates in the the equation:
dP/dt = (B(t) – d(t))*P
So on number 4 I end up with dP/dt = (AP – 0.01)*P where A is the proportional constant of the birthrate to the population. When I integrate this I end up with a crazy equation with P to the 100th power like this:
(0.01P-1)/P^100 =Ae^t
The numbers get pretty difficult from there and if I’m thinking about it correctly then I believe doomsday would be at time t = ln(200^100), so I’m just wondering if this is a correct setup and the numbers are just really high or if I need to rethink how I put this problem together.
That is the right way to set these problems up: start assuming that they are a general population model, and the slope field will tell you what special kind they are. You did the right reasoning. If you don’t want to deal with powers on the side, send the constants to the
side, send the constants to the  side; yes, that simple.
side; yes, that simple.
Solve it afterwards but, when we ask you about the doomsday situation… are you sure there will be doomsday with these initial conditions? This is the trick for this one.
For number 5, could you help me out with what the initial equation would be? I’m having trouble interpreting the information given into an equation. Would it just be dv/dt = -20 and then v(t) = -20t +c? This seems way too simple.
I know that I want to figure out an equation for x(t) since 75m is given in the problem statement. However if the equation which I just posted is correct, then I don’t see how to find c because we don’t know t. But the c is needed for further integration from v(t) to x(t) to be possible.
Yes, that simple. The difficulty here comes (as you realized later on) when you want to find the value of with the clues spread on the statement of the problem. Note that
with the clues spread on the statement of the problem. Note that  is precisely the speed at which the car was going before it started decelerating. You need to leave it alone until dealing with the motion
is precisely the speed at which the car was going before it started decelerating. You need to leave it alone until dealing with the motion 
In the example we did in class on 2/10, a ball was dropped from a plane at 15000 ft and we were trying to find limiting speed. Air resistance was given. Why did you set the problem up as
m(dv/dt)=(m)(g)-rho(m)(v) here gravity is positive when dropping a object.
Why, in your comment above is your gravity negative if the object is falling?
Both are correct (see the corresponding explanation in page 101). The only difference is how you interpret and input your initial values. I am sure y’all have seen many examples like this is your Physics classes. In our diffeq is exactly the same.