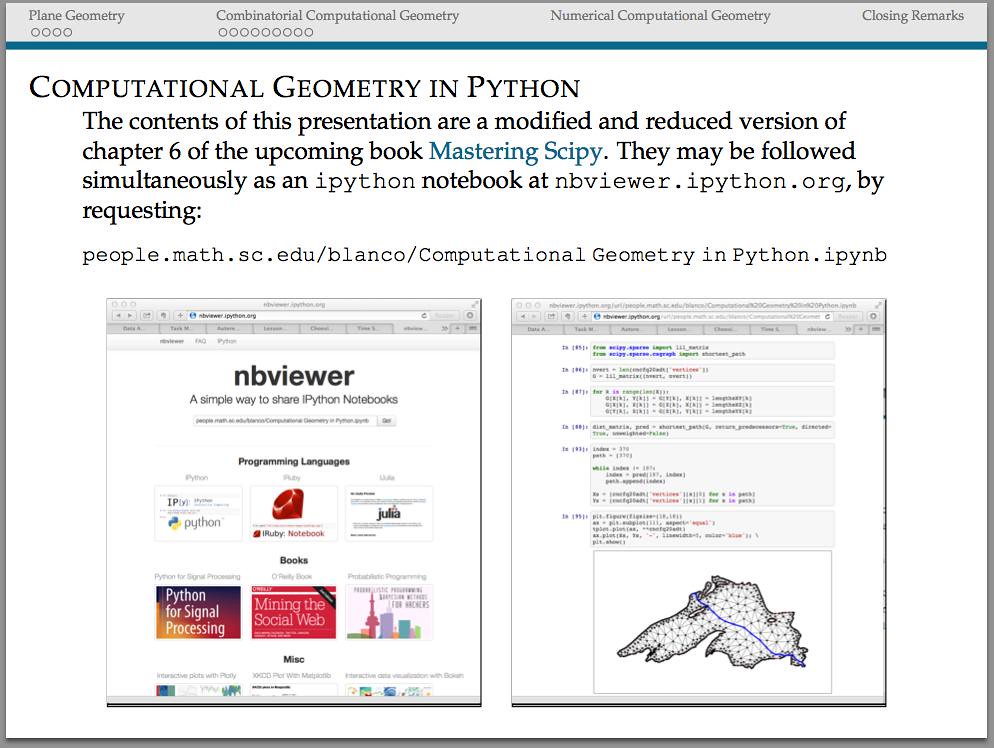
Archive
Book presentation at the USC Python Users Group
Areas of Mathematics
For one of my upcoming talks I am trying to include an exhaustive mindmap showing the different areas of Mathematics, and somehow, how they relate to each other. Most of the information I am using has been processed from years of exposure in the field, and a bit of help from Wikipedia.

But I am not entirely happy with what I see: my lack of training in the area of Combinatorics results in a rather dry treatment of that part of the mindmap, for example. I am afraid that the same could be told about other parts of the diagram. Any help from the reader to clarify and polish this information will be very much appreciated.
And as a bonus, I included a script to generate the diagram with the aid of the tikz libraries.
\tikzstyle{level 2 concept}+=[sibling angle=40]
\begin{tikzpicture}[scale=0.49, transform shape]
\path[mindmap,concept color=black,text=white]
node[concept] {Pure Mathematics} [clockwise from=45]
child[concept color=DeepSkyBlue4]{
node[concept] {Analysis} [clockwise from=180]
child {
node[concept] {Multivariate \& Vector Calculus}
[clockwise from=120]
child {node[concept] {ODEs}}}
child { node[concept] {Functional Analysis}}
child { node[concept] {Measure Theory}}
child { node[concept] {Calculus of Variations}}
child { node[concept] {Harmonic Analysis}}
child { node[concept] {Complex Analysis}}
child { node[concept] {Stochastic Analysis}}
child { node[concept] {Geometric Analysis}
[clockwise from=-40]
child {node[concept] {PDEs}}}}
child[concept color=black!50!green, grow=-40]{
node[concept] {Combinatorics} [clockwise from=10]
child {node[concept] {Enumerative}}
child {node[concept] {Extremal}}
child {node[concept] {Graph Theory}}}
child[concept color=black!25!red, grow=-90]{
node[concept] {Geometry} [clockwise from=-30]
child {node[concept] {Convex Geometry}}
child {node[concept] {Differential Geometry}}
child {node[concept] {Manifolds}}
child {node[concept,color=black!50!green!50!red,text=white] {Discrete Geometry}}
child {
node[concept] {Topology} [clockwise from=-150]
child {node [concept,color=black!25!red!50!brown,text=white]
{Algebraic Topology}}}}
child[concept color=brown,grow=140]{
node[concept] {Algebra} [counterclockwise from=70]
child {node[concept] {Elementary}}
child {node[concept] {Number Theory}}
child {node[concept] {Abstract} [clockwise from=180]
child {node[concept,color=red!25!brown,text=white] {Algebraic Geometry}}}
child {node[concept] {Linear}}}
node[extra concept,concept color=black] at (200:5) {Applied Mathematics}
child[grow=145,concept color=black!50!yellow] {
node[concept] {Probability} [clockwise from=180]
child {node[concept] {Stochastic Processes}}}
child[grow=175,concept color=black!50!yellow] {node[concept] {Statistics}}
child[grow=205,concept color=black!50!yellow] {node[concept] {Numerical Analysis}}
child[grow=235,concept color=black!50!yellow] {node[concept] {Symbolic Computation}};
\end{tikzpicture}
More on Lindenmayer Systems
We briefly explored Lindenmayer systems (or L-systems) in an old post: Toying with Basic Fractals. We quickly reviewed this method for creation of an approximation to fractals, and displayed an example (the Koch snowflake) based on tikz libraries.
I would like to show a few more examples of beautiful curves generated with this technique, together with their generating axiom, rules and parameters. Feel free to click on each of the images below to download a larger version.
Note that any coding language with plotting capabilities should be able to tackle this project. I used once again tikz for , but this time with the tikzlibrary lindenmayersystems.
Would you like to experiment a little with axioms, rules and parameters, and obtain some new pleasant curves with this method? If the mathematical properties of the fractal that they approximate are interesting enough, I bet you could attach your name to them. Like the astronomer that finds through her telescope a new object in the sky, or the zoologist that discover a new species of spider in the forest.
Some results related to the Feuerbach Point
Given a triangle the circle that goes through the midpoints of each side,
is called the Feuerbach circle. It has very surprising properties:
- It also goes through the feet of the heights, points
- If
denotes the orthocenter of the triangle, then the Feuerbach circle also goes through the midpoints of the segments
For this reason, the Feuerbach circle is also called the nine-point circle.
- The center of the Feuerbach circle is the midpoint between the orthocenter and circumcenter of the triangle.
- The area of the circumcircle is precisely four times the area of the Feuerbach circle.
Most of these results are easily shown with sympy without the need to resort to Gröbner bases or Ritt-Wu techniques. As usual, we realize that the properties are independent of rotation, translation or dilation, and so we may assume that the vertices of the triangle are and
for some positive parameters
To prove the last statement, for instance we may issue the following:
>>> import sympy
>>> from sympy import *
>>> A=Point(0,0)
>>> B=Point(1,0)
>>> r,s=var('r,s')
>>> C=Point(r,s)
>>> D=Segment(A,B).midpoint
>>> E=Segment(B,C).midpoint
>>> F=Segment(A,C).midpoint
>>> simplify(Triangle(A,B,C).circumcircle.area/Triangle(D,E,F).circumcircle.area)
4
But probably the most amazing property of the nine-point circle, is the fact that it is tangent to the incircle of the triangle. With exception of the case of equilateral triangles, both circles intersect only at one point: the so-called Feuerbach point.
An Automatic Geometric Proof
We are familiar with that result that states that, on any given triangle, the circumcenter, centroid and orthocenter are always collinear. I would like to illustrate how to use Gröbner bases theory to prove that the incenter also belongs in the previous line, provided the triangle is isosceles.
We start, as usual, indicating that this property is independent of shifts, rotations or dilations, and therefore we may assume that the isosceles triangle has one vertex at , another vertex at
and the third vertex at
for some value
In that case, we will need to work on the polynomial ring
since we need the parameter
free, the variables
and
are used to input the conditions for the circumcenter of the triangle, the variables
and
for centroid, and the variables
and
for the incenter (note that we do not need to use the orthocenter in this case).
We may obtain all six conditions by using sympy, as follows:
>>> import sympy
>>> from sympy import *
>>> A=Point(0,0)
>>> B=Point(1,0)
>>> s=symbols("s",real=True,positive=True)
>>> C=Point(1/2.,s)
>>> T=Triangle(A,B,C)
>>> T.circumcenter
Point(1/2, (4*s**2 - 1)/(8*s))
>>> T.centroid
Point(1/2, s/3)
>>> T.incenter
Point(1/2, s/(sqrt(4*s**2 + 1) + 1))
This translates into the following polynomials
The hypothesis polynomial comes simply from asking whether the slope of the line through two of those centers is the same as the slope of the line through another choice of two centers; we could use then, for example, It only remains to compute the Gröbner basis of the ideal
Let us use SageMath for this task:
sage: R.<s,x1,x2,x3,y1,y2,y3,z>=PolynomialRing(QQ,8,order='lex') sage: h=[2*x1-1,8*r*y1-4*r**2+1,2*x2-1,3*y2-r,2*x3-1,(4*r*y3+1)**2-4*r**2-1] sage: g=(x2-x1)*(y3-y1)-(x3-x1)*(y2-y1) sage: I=R.ideal(1-z*g,*h) sage: I.groebner_basis() [1]
This proves the result.
Sympy should suffice
I have just received a copy of Instant SymPy Starter, by Ronan Lamy—a no-nonsense guide to the main properties of SymPy, the Python library for symbolic mathematics. This short monograph packs everything you should need, with neat examples included, in about 50 pages. Well-worth its money.
To celebrate, I would like to pose a few coding challenges on the use of this library, based on a fun geometric puzzle from cut-the-knot: Rhombus in Circles
Segments
and
are equal. Lines
and
intersect at
Form four circumcircles:
Prove that the circumcenters
form a rhombus, with
Note that if this construction works, it must do so independently of translations, rotations and dilations. We may then assume that is the origin, that the segments have length one,
and that for some parameters
it is
We let SymPy take care of the computation of circumcenters:
import sympy
from sympy import *
# Point definitions
M=Point(0,0)
A=Point(2,0)
B=Point(1,0)
a,theta=symbols('a,theta',real=True,positive=True)
C=Point((a+1)*cos(theta),(a+1)*sin(theta))
D=Point(a*cos(theta),a*sin(theta))
#Circumcenters
E=Triangle(A,C,M).circumcenter
F=Triangle(A,D,M).circumcenter
G=Triangle(B,D,M).circumcenter
H=Triangle(B,C,M).circumcenter
Finding that the alternate angles are equal in the quadrilateral is pretty straightforward:
In [11]: P=Polygon(E,F,G,H) In [12]: P.angles[E]==P.angles[G] Out[12]: True In [13]: P.angles[F]==P.angles[H] Out[13]: True
To prove it a rhombus, the two sides that coincide on each angle must be equal. This presents us with the first challenge: Note for example that if we naively ask SymPy whether the triangle is equilateral, we get a False statement:
In [14]: Triangle(E,F,G).is_equilateral() Out[14]: False In [15]: F.distance(E) Out[15]: Abs((a/2 - cos(theta))/sin(theta) - (a - 2*cos(theta) + 1)/(2*sin(theta))) In [16]: F.distance(G) Out[16]: sqrt(((a/2 - cos(theta))/sin(theta) - (a - cos(theta))/(2*sin(theta)))**2 + 1/4)
Part of the reason is that we have not indicated anywhere that the parameter theta is to be strictly bounded above by (we did indicate that it must be strictly positive). The other reason is that SymPy does not handle identities well, unless the expressions to be evaluated are perfectly simplified. For example, if we trust the routines of simplification of trigonometric expressions alone, we will not be able to resolve this problem with this technique:
In [17]: trigsimp(F.distance(E)-F.distance(G),deep=True)==0 Out[17]: False
Finding that with SymPy is not that easy either. This is the second challenge.
How would the reader resolve this situation?
Have a child, plant a tree, write a book
Or more importantly: rear your children to become nice people, water those trees, and make sure that your books make a good impact.
I recently enjoyed the rare pleasure of having a child (my first!) and publishing a book almost at the same time. Since this post belongs in my professional blog, I will exclusively comment on the latter: Learning SciPy for Numerical and Scientific Computing, published by Packt in a series of technical books focusing on Open Source software.
Keep in mind that the book is for a very specialized audience: not only do you need a basic knowledge of Python, but also a somewhat advanced command of mathematics/physics, and an interest in engineering or scientific applications. This is an excerpt of the detailed description of the monograph, as it reads in the publisher’s page:
It is essential to incorporate workflow data and code from various sources in order to create fast and effective algorithms to solve complex problems in science and engineering. Data is coming at us faster, dirtier, and at an ever increasing rate. There is no need to employ difficult-to-maintain code, or expensive mathematical engines to solve your numerical computations anymore. SciPy guarantees fast, accurate, and easy-to-code solutions to your numerical and scientific computing applications.
Learning SciPy for Numerical and Scientific Computing unveils secrets to some of the most critical mathematical and scientific computing problems and will play an instrumental role in supporting your research. The book will teach you how to quickly and efficiently use different modules and routines from the SciPy library to cover the vast scope of numerical mathematics with its simplistic practical approach that is easy to follow.
The book starts with a brief description of the SciPy libraries, showing practical demonstrations for acquiring and installing them on your system. This is followed by the second chapter which is a fun and fast-paced primer to array creation, manipulation, and problem-solving based on these techniques.
The rest of the chapters describe the use of all different modules and routines from the SciPy libraries, through the scope of different branches of numerical mathematics. Each big field is represented: numerical analysis, linear algebra, statistics, signal processing, and computational geometry. And for each of these fields all possibilities are illustrated with clear syntax, and plenty of examples. The book then presents combinations of all these techniques to the solution of research problems in real-life scenarios for different sciences or engineering — from image compression, biological classification of species, control theory, design of wings, to structural analysis of oxides.
The book is also being sold online in Amazon, where it has been received with pretty good reviews. I have found other random reviews elsewhere, with similar welcoming comments:
- Artificial Intelligence in Motion by Marcel Caraciolo
- The Endeavour, by John D. Cook
Buy my book!
Well, ok, it is not my book technically, but I am one of the authors of one of the chapters. And no, as far as I know, I don’t get a dime of the sales in concept of copyright or anything else.
As the title suggests (Modeling Nanoscale Imaging in Electron Microscopy), this book presents some recent advances that have been made using mathematical methods to resolve problems in electron microscopy. With improvements in hardware-based aberration software significantly expanding the nanoscale imaging capabilities of scanning transmission electron microscopes (STEM), these mathematical models can replace some labor intensive procedures used to operate and maintain STEMs. This book, the first in its field since 1998, covers relevant concepts such as super-resolution techniques (that’s my contribution!), special de-noising methods, application of mathematical/statistical learning theory, and compressed sensing.
We even got a nice review in Physics Today by Les Allen, no less!
Imaging with electrons, in particular scanning transmission electron microscopy (STEM), is now in widespread use in the physical and biological sciences. And its importance will only grow as nanotechnology and nano-Biology continue to flourish. Many applications of electron microscopy are testing the limits of current imaging capabilities and highlight the need for further technological improvements. For example, high throughput in the combinatorial chemical synthesis of catalysts demands automated imaging. The handling of noisy data also calls for new approaches, particularly because low electron doses are used for sensitive samples such as biological and organic specimens.
Modeling Nanoscale Imaging in Electron Microscopy addresses all those issues and more. Edited by Thomas Vogt and Peter Binev at the University of South Carolina (USC) and Wolfgang Dahmen at RWTH Aachen University in Germany, the book came out of a series of workshops organized by the Interdisciplinary Mathematics Institute and the NanoCenter at USC. Those sessions took the unusual but innovative approach of bringing together electron microscopists, engineers, physicists, mathematicians, and even a philosopher to discuss new strategies for image analysis in electron microscopy.
In six chapters, the editors tackle the ambitious challenge of bridging the gap between high-level applied mathematics and experimental electron microscopy. They have met the challenge admirably. I believe that high-resolution electron microscopy is at a point where it will benefit considerably from an influx of new mathematical approaches, daunting as they may seem; in that regard Modeling Nanoscale Imaging in Electron Microscopy is a major step forward. Some sections present a level of mathematical sophistication seldom encountered in the experimentally focused electron-microscopy literature.
The first chapter, by philosopher of science Michael Dickson, looks at the big picture by raising the question of how we perceive nano-structures and suggesting that a Kantian approach would be fruitful. The book then moves into a review of the application of STEM to nanoscale systems, by Nigel Browning, a leading experimentalist in the field, and other well-known experts. Using case studies, the authors show how beam-sensitive samples can be studied with high spatial resolution, provided one controls the beam dose and establishes the experimental parameters that allow for the optimum dose.The third chapter, written by image-processing experts Sarah Haigh and Angus Kirkland, addresses the reconstruction, from atomic-resolution images, of the wave at the exit surface of a specimen. The exit surface wave is a fundamental quantity containing not only amplitude (image) information but also phase information that is often intimately related to the atomic-level structure of the specimen. The next two chapters, by Binev and other experts, are based on work carried out using the experimental and computational resources available at USC. Examples in chapter four address the mathematical foundations of compressed sensing as applied to electron microscopy, and in particular high-angle annular dark-field STEM. That emerging approach uses randomness to extract the essential content from low-information signals. Chapter five eloquently discusses the efficacy of analyzing several low-dose images with specially adapted digital-image-processing techniques that allow one to keep the cumulative electron dose low and still achieve acceptable resolution.
The book concludes with a wide-ranging discussion by mathematicians Amit Singer and Yoel Shkolnisky on the reconstruction of a three-dimensional object via projected data taken at random and initially unknown object orientations. The discussion is an extension of the authors’ globally consistent angular reconstitution approach for recovering the structure of a macromolecule using cryo-electron microscopy. That work is also applicable to the new generation of x-ray free-electron lasers, which have similar prospective applications, and illustrates nicely the importance of applied mathematics in the physical sciences.
Modeling Nanoscale Imaging in Electron Microscopy will be an important resource for graduate students and researchers in the area of high-resolution electron microscopy.
(Les J. Allen, Physics Today, Vol. 65 (5), May, 2012)

|

|

|
| Table of contents | Preface | Sample chapter |
Trigonometry
I have just realized that I haven’t posted a good puzzle here in a long time, so here it goes one on Trigonometry, that the average student of Calculus should be able to tackle: you can use anything you think it could help: derivatives, symmetry, periodicity, integration, summation, go to several variables, differential equations, etc
Prove that, for all real values
it is
or, in a more compact notation,
Edge detection: The Convolution Approach
Today I would like to show a very basic technique of detection based on simple convolution of an image with small kernels (masks). The purpose of these kernels is to enhance certain properties of the image at each pixel. What properties? Those that define what means to be an edge, in a differential calculus way—exactly as it was defined in the description of the Canny edge detector. The big idea is to assign to each pixel a numerical value that expresses its strength as an edge: positive if we suspect that such structure is present at that location, negative if not, and zero if the image is locally flat around that point. Masks can be designed so that they mimic the effect of differential operators, but these can be terribly complicated and give rise to large matrices.
The first approaches were performed with simple kernels. For example, Faler came up with the following four simple masks that emulate differentiation:
Note that, adding all the values of each matrix, one obtains zero. This is consistent with the third property required for our kernels: in the event of a locally flat area around a given pixel, convolution with any of these will offer a value of zero.
So you want to be an Applied Mathematician
The way of the Applied Mathematician is one full of challenging and interesting problems. We thrive by association with the Pure Mathematician, and at the same time with the no-nonsense, hands-in, hard-core Engineer. But not everything is happy in Applied Mathematician land: every now and then, we receive the disregard of other professionals that mistake either our background, or our efficiency at attacking real-life problems.
I heard from a colleague (an Algebrist) complains that Applied Mathematicians did nothing but code solutions of partial differential equations in Fortran—his skewed view came up after a naïve observation of a few graduate students working on a project. The truth could not be further from this claim: we do indeed occasionally solve PDEs in Fortran—I give you that—and we are not ashamed to admit it. But before that job has to be addressed, we have gone through a great deal of thinking on how to better code this simple problem. And you would not believe the huge amount of deep Mathematics that are involved in this journey: everything from high-level Linear Algebra, Calculus of Variations, Harmonic Analysis, Differential Geometry, Microlocal Analysis, Functional Analysis, Dynamical Systems, the Theory of Distributions, etc. Not only are we familiar with the basic background on all those fields, but also we are supposed to be able to perform serious research on any of them at a given time.
My soon-to-be-converted Algebrist friend challenged me—not without a hint of smugness in his voice—to illustrate what was my last project at that time. This was one revolving around the idea of frames (think of it as redundant bases if you please), and needed proving a couple of inequalities involving sequences of functions in —spaces, which we attacked using a beautiful technique: Bellman functions. About ninety minutes later he conceded defeat in front of the board where the math was displayed. He promptly admitted that this was no Fortran code, and showed a newfound respect and reverence for the trade.
It doesn’t hurt either that the kind of problems that we attack are more likely to attract funding. And collaboration. And to be noticed in the press.
Alright, so some of you are sold already. What is the next step? I am assuming that at his point you own your Calculus, Analysis, Probability and Statistics, Linear Programming, Topology, Geometry, Physics and you are able to solve most known ODEs. From here, as with any other field, my recommendation is to slowly build a Batman belt: acquire and devour a sequence of books and scientific articles, until you are very familiar with their contents. When facing a new problem, you should be able to recall from your Batman belt what technique could work best, in which book(s) you could get some references, and how it has been used in the past for related problems.
Following these lines, I have included below an interesting collection with the absolutely essential books that, in my opinion, every Applied Mathematician should start studying:
The ultimate metapuzzle
If you have been following this blog for a while, you already know of my fascination with metapuzzles. I have recently found one of the most beautiful examples of these riddles in this August’s edition of Ponder This, and following the advice of Travis, I will leave it completely open for the readers to give it a go. Enjoy!
A mathematician wanted to teach his children the value of cooperation, so he told them the following:
“I chose a secret triangle for which the lengths of its sides are all integers.
To you my dear son Charlie, I am giving the triangle’s perimeter. And to you, my beloved daughter Ariella, I am giving its area.
Since you are both such talented mathematicians, I’m sure that together you can find the lengths of the triangle’s sides.”
Instead of working together, Charlie and Ariella had the following conversation after their father gave each of them the information he promised.
Charlie: “Alas, I cannot deduce the lengths of the sides from my knowledge of the perimeter.”
Ariella: “I do not know the perimeter, but I cannot deduce the lengths of the sides from just knowing the area. Maybe our father is right and we should cooperate after all.”
Charlie: “Oh no, no need. Now I know the lengths of the sides.”
Ariella: “Well, now I know them as well.”
Find the lengths of the triangle’s sides.
Where are the powers of two?
The following construction gives an interesting pairing map between the positive integers and the lattice of integer-valued points in the plane:
- Place
at the origin.
- For each level
populate the
points of the plane on the square with vertices
starting from
at the position
and going counter-clockwise.
After pairing enough positive integers on the lattice, pay attention to the powers of two: they all seem to be located on the same two horizontal lines: and
Is this statement true?
Geolocation
Recall the First Spherical Law of Cosines:
Given a unit sphere, a spherical triangle on the surface of the sphere is defined by the great circles connecting three points
,
, and
on the sphere. If the lengths of these three sides are
(from
to
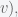
(from
to
and
(from
to
and the angle of the corner opposite
is
then
In any decent device and for most computer languages, this formula should give well-conditioned results down to distances as small as around three feet, and thus can be used to compute an accurate geodetic distance between two given points in the surface of the Earth (well, ok, assuming the Earth is a perfect sphere). The geodetic form of the law of cosines is rearranged from the canonical one so that the latitude can be used directly, rather than the colatitude, and reads as follows: Given points and
with positions
and
respectively, the distance
between the two points is given by the following formula.
where is the radius of the Earth in miles (well, ok, the average radius of the Earth…)
A nice application of this formula can be used for geolocation purposes, and I recently had the pleasure to assist a software company (thumb-mobile.com) to write such functionality for one of their clients.
 |
 |
 |
Go to www.lizardsthicket.com in your mobile device, and click on “Find a Location.” This fires up the location services of your browser. When you accept, your latitude and longitude are tracked. After a fast, reliable and resource-efficient algorithm, the page offers the location of the restaurant from the Lizard’s chain that is closest to you. Simple, right?
Apollonian gaskets and circle inversion fractals
Recall the definition of an iterated function system (IFS), and how on occasion, their attractors are fractal sets. What happens when we allow more general functions instead of mere affine maps?

The key to the design of this amazing fractal is in the notion of limit sets of circle inversions.
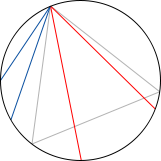
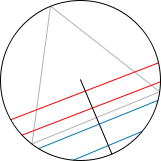
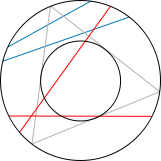
Bertrand Paradox
Classically, we define the probability of an event as the ratio of the favorable cases, over the number of all possible cases. Of course, these possible cases need to be all equally likely. This works great for discrete settings, like dice rolls, card games, etc. But when facing non-discrete cases, this definition needs to be revised, as the following example shows:
Consider an equilateral triangle inscribed in a circle. Suppose a chord of the circle is chosen at random. What is the probability that the chord is longer than a side of the triangle?
First example Second example Third example
Voronoi mosaics
While looking for ideas to implement voronoi in sage, I stumbled upon a beautiful paper written by a group of japanese computer graphic professionals from the universities of Hokkaido and Tokyo: A Method for Creating Mosaic Images Using Voronoi Diagrams. The first step of their algorithm is simple yet brilliant: Start with any given image, and superimpose an hexagonal tiling of the plane. By a clever approximation scheme, modify the tiling to become a voronoi diagram that adaptively minimizes some approximation error. As a consequence, the resulting voronoi diagram is somehow adapted to the desired contours of the original image.
 |
 |
 |
 |
| (Fig. 1) | (Fig. 2) | (Fig. 3) | (Fig. 4) |
In a second step, they manually adjust the Voronoi image interactively by moving, adding, or deleting sites. They also take the liberty of adding visual effects by hand: emphasizing the outlines and color variations in each Voronoi region, so they look like actual pieces of stained glass (Fig. 4).
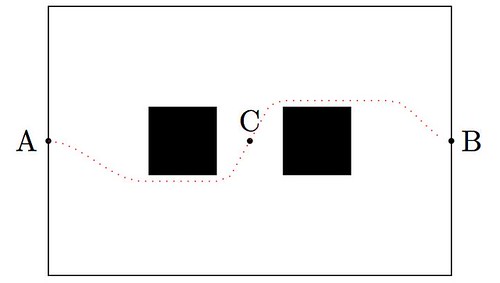
Triangulations
As part of a project developed by Professor Bradley J. Lucier, to code a PDE solver written in scheme, I worked in some algorithms to perform “good triangulations” of polygons with holes (“good triangulations” meaning here, those where all the triangles have their three angles as close to 60º as possible). I obtained the necessary theoretical background and coding strategies from the following references:
- Mark de Berg et al., “Computational Geometry by Example.“
- Francis Chin and Cao An Wang, “Finding the Constrained Delaunay Triangulation and Constrained Voronoi Diagram of a simple Polygon in Linear Time.“
- Joseph O’Rourke, “Computational Geometry in C.“
- Jim Ruppert, “A Delaunay Refinement Algorithm for Quality 2-dimensional Mesh Generation.“
Mechanical Geometry Theorem Proving
In 1977, Professor Wen-Tsun Wu succeeded in developing a method of mechanical geometry theorem proving. This method has been applied to prove or even discover hundreds of non-trivial difficult theorems in elementary and differential geometries on a computer in an almost trivial manner. Usign Ritt’s differential algebra, Wu established a method for solving algebraic and differential equations by transforming an equation system in the general form to equation systems in triangular form. This is the Ritt-Wu decomposition algorithm, that later on was shown to be equivalent to perform a series of operations on ideals, very easily carried out by means of Gröbner basis manipulation.
I wrote a script in MAPLE to perform evaluations of the validity of some simple theorems in Euclidean Geometry, and wrote a small paper (in Spanish) on one of my findings, that was published in Bol. Asoc. Prof. Puig Adams, in October’99: “Sobre demostración automática de un problema geométrico“.
The example I cover in that short article can be seen below.
Given: Circles
,
that intersect each other in points
and
, and given points
,
in circle
, consider line
through
and
, and line
through
and
. The intersections of line
with circle
are
and
. The intersections of line
with circle
are
and
. Consider the segments
(connecting
with
) and
(connecting
with
).
To prove: Segments
and
are parallel.