Computational Geometry in Python

To illustrate a few advantages of the scipy stack in one of my upcoming talks, I have placed an ipython notebook with (a reduced version of) the current draft of Chapter 6 (Computational Geometry) of my upcoming book: Mastering SciPy.

The raw ipynb can be downloaded from my github repository [blancosilva/Mastering-Scipy/], or viewed directly from the nbviewer at [this other link]

I also made a selection with some fun examples for the talk. You can download the presentation by clicking in the image above.

Enjoy!

Searching (again!?) for the SS Central America

On Tuesday, September 8th 1857, the steamboat SS Central America left Havana at 9 AM for New York, carrying about 600 passengers and crew members. Inside of this vessel, there was stowed a very precious cargo: a set of manuscripts by John James Audubon, and three tons of gold bars and coins. The manuscripts documented an expedition through the yet uncharted southwestern United States and California, and contained 200 sketches and paintings of its wildlife. The gold, fruit of many years of prospecting and mining during the California Gold Rush, was meant to start anew the lives of many of the passengers aboard.

On the 9th, the vessel ran into a storm which developed into a hurricane. The steamboat endured four hard days at sea, and by Saturday morning the ship was doomed. The captain arranged to have women and children taken off to the brig Marine, which offered them assistance at about noon. In spite of the efforts of the remaining crew and passengers to save the ship, the inevitable happened at about 8 PM that same day. The wreck claimed the lives of 425 men, and carried the valuable cargo to the bottom of the sea.

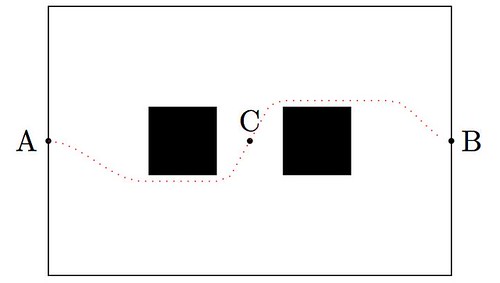
It was not until late 1980s that technology allowed recovery of shipwrecks at deep sea. But no technology would be of any help without an accurate location of the site. In the following paragraphs we would like to illustrate the power of the scipy stack by performing a simple simulation, that ultimately creates a dataset of possible locations for the wreck of the SS Central America, and mines the data to attempt to pinpoint the most probable target.

We simulate several possible paths of the steamboat (say 10,000 randomly generated possibilities), between 7:00 AM on Saturday, and 13 hours later, at 8:00 pm on Sunday. At 7:00 AM on that Saturday the ship’s captain, William Herndon, took a celestial fix and verbally relayed the position to the schooner El Dorado. The fix was 31º25′ North, 77º10′ West. Because the ship was not operative at that point—no engine, no sails—, for the next thirteen hours its course was solely subjected to the effect of ocean current and winds. With enough information, it is possible to model the drift and leeway on different possible paths.

Jotto (5-letter Mastermind) in the NAO robot

I would like to show how to code the NAO robot to beat us at Jotto (5-letter Mastermind) with python in Choregraphe. I will employ a brute force technique that does not require any knowledge of the English language, the frequency of its letters, or smart combinations of vowels and consonants to try to minimize the number of attempts. It goes like this:

1. Gather all 5-letter words with no repeated letters in a list.
2. Choose a random word from that list—your guess—, and ask it to be scored ala Mastermind.
3. Filter through the list all words that share the same score with your guess; discard the rest.
4. Go back to step 2 and repeat until the target word is found.

Coding this strategy in python requires only four variables:

• whole_dict: the list with all the words
• step = [x for x in whole_dict]: A copy of whole_dict, which is going to be shortened on each step (hence the name). Note that stating step = whole_dict will change the contents of whole_dict when we change the contents of step — not a good idea.
• guess = random.choice(step): A random choice from the list step.
• score: A string containing the two digits we obtain after scoring the guess. The first digit indicates the number of correct letters in the same position as the target word; the second digit indicates the number of correct letters in the wrong position.
• attempts: optional. The number of attempts at guessing words. For quality control purposes.

At this point, I urge the reader to stop reading the post and try to implement this strategy as a simple script. When done, come back to see how it can be coded in the NAO robot.

Robot stories

Every summer before school was over, I was assigned a list of books to read. Mostly nonfiction and historical fiction, but in fourth grade there that was that first science fiction book. I often remember how that book made me feel, and marvel at the impact that it had in my life. I had read some science fiction before—Well’s Time Traveller and War of the Worlds—but this was different. This was a book with witty and thought-provoking short stories by Isaac Asimov. Each of them delivered drama, comedy, mystery and a surprise ending in about ten pages. And they had robots. And those robots had personalities, in spite of their very simple programming: The Three Laws of Robotics.

1. A robot may not injure a human being or, through inaction, allow a human being to come to harm.
2. A robot must obey the orders given to it by human beings, except where such orders would conflict with the First Law.
3. A robot must protect its own existence as long as such protection does not conflict with the First or Second Law.

Back in the 1980s, robotics—understood as autonomous mechanical thinking—was no more than a dream. A wonderful dream that fueled many children’s imaginations and probably shaped the career choices of some. I know in my case it did.

Fast forward some thirty-odd years, when I met Astro: one of three research robots manufactured by the French company Aldebaran. This NAO robot found its way into the computer science classroom of Tom Simpson in Heathwood Hall Episcopal School, and quickly learned to navigate mazes, recognize some student’s faces and names, and even dance the Macarena! It did so with effortless coding: a basic command of the computer language python, and some idea of object oriented programming.

I could not let this opportunity pass. I created a small undergraduate team with Danielle Talley from USC (a brilliant sophomore in computer engineering, with a minor in music), and two math majors from Morris College: my Geometry expert Fabian Maple, and a McGyver-style problem solver, Wesley Alexander. Wesley and Fabian are supported by a Department of Energy-Environmental Management grant to Morris College, which funds their summer research experience at USC. Danielle is funded by the National Science Foundation through the Louis Stokes South Carolina-Alliance for Minority Participation (LS-SCAMP).

They spent the best of their first week on this project completing a basic programming course online. At the same time, the four of us reviewed some of the mathematical tools needed to teach Astro new tricks: basic algebra and trigonometry, basic geometry, and basic calculus and statistics. The emphasis—I need to point out in case you missed it—is in the word basic.

Talk the talk

The psychologist seated herself and watched Herbie narrowly as he took a chair at the other side of the table and went through the three books systematically.

At the end of half an hour, he put them down, “Of course, I know why you brought these.”

The corner of Dr. Calvin’s lip twitched, “I was afraid you would. It’s difficult to work with you, Herbie. You’re always a step ahead of me.”

“It’s the same with these books, you know, as with the others. They just don’t interest me. There’s nothing to your textbooks. Your science is just a mass of collected data plastered together by makeshift theory — and all so incredibly simple, that it’s scarcely worth bothering about.”

“It’s your fiction that interests me. Your studies of the interplay of human motives and emotions” – his mighty hand gestured vaguely as he sought the proper words.

Liar!
— Isaac Asimov

Astro can understand what I say, and maintain conversations with me. He has four microphones for voice recognition and sound localization, and two speakers for text-to-speech synthesis. But he sometimes gets confused: I say “acute”, and he understands “abide,” for example. This might sound frustrating by all standards. But mathematicians can’t be judged by any reasonable standard. Far from seeing this as a shortcoming, my team used as motivation the mechanics behind his speech recognition functionality, and they wrote some code to turn him into an expert Mastermind player.

Wait, what? How are these two things possibly connected?

Since Astro’s hearing is far from perfect, when he hears a word which is not clear, he gathers a short list of possible candidates. He then chooses the most likely guess based upon different considerations—using clues from context, for example. Based on similar strategies, he can be taught to be a perfect player of 5-letter-word Mastermind: Pick any five-letter word in the English language. Any word, provided it has no repeated letters. Astro chooses one random word as his first guess, and requests a score like in Mastermind.

To illustrate this process, I will show you how the game went when I chose Fabian’s favorite word: “acute.”

Astro: Is it firth?
Me   : NO
Astro: How many letters of my guess are in your word, in the right position?
       How many letters of my guess are in your word, in the wrong position?
Me   : 1, 0
Astro: Is it foams?
Me   : NO
Astro: How many letters of my guess are in your word, in the right position?
       How many letters of my guess are in your word, in the wrong position?
Me   : 0, 1
Astro: Is it junta?
Me   : NO
Astro: How many letters of my guess are in your word, in the right position?
       How many letters of my guess are in your word, in the wrong position?
Me   : 1, 2
Astro: Is it acute?
Me   : YES
Astro: Wonderful, I found it in 4 attempts!

I don’t want to get too technical here, but will mention some of the ideas. The main algorithm is based on techniques of numerical root finding and solving nonlinear equations — nothing complex: high-school level bracketing by bisection, or Newton’s method. To design better winning strategies, my team exploits the benefits of randomness. The analysis of this part is done with basic probability and statistics.

Walk the walk

Donovan’s pencil pointed nervously. “The red cross is the selenium pool. You marked it yourself.”

“Which one is it?” interrupted Powell. “There were three that MacDougal located for us before he left.”

“I sent Speedy to the nearest, naturally; seventeen miles away. But what difference does that make?” There was tension in his voice. “There are penciled dots that mark Speedy’s position.”

And for the first time Powell’s artificial aplomb was shaken and his hands shot forward for the man.

“Are you serious? This is impossible.”

“There it is,” growled Donovan.

The little dots that marked the position formed a rough circle about the red cross of the selenium pool. And Powell’s fingers went to his brown mustache, the unfailing signal of anxiety.

Donovan added: “In the two hours I checked on him, he circled that damned pool four times. It seems likely to me that he’ll keep that up forever. Do you realize the position we’re in?”

Runaround
— Isaac Asimov

Astro moves around too. It does so thanks to a sophisticated system combining one accelerometer, one gyrometer and four ultrasonic sensors that provide him with stability and positioning within space. He also enjoys eight force-sensing resistors and two bumpers. And that is only for his legs! He can move his arms, bend his elbows, open and close his hands, or move his torso and neck (up to 25 degrees of freedom for the combination of all possible joints). Out of the box, and without much effort, he can be coded to walk around, although in a mechanical way: He moves forward a few feet, stops, rotates in place or steps to a side, etc. A very naïve way to go from A to B retrieving an object at C, could be easily coded in this fashion as the diagram shows:

Fabian and Wesley devised a different way to code Astro taking full advantage of his inertial measurement unit. This will allow him to move around smoothly, almost like a human would. The key to their success? Polynomial interpolation and plane geometry. For advanced solutions, they need to learn about splines, curvature, and optimization. Nothing they can’t handle.

Sing me a song

He said he could manage three hours and Mortenson said that would be perfect when I gave him the news. We picked a night when she was going to be singing Bach or Handel or one of those old piano-bangers, and was going to have a long and impressive solo.

Mortenson went to the church that night and, of course, I went too. I felt responsible for what was going to happen and I thought I had better oversee the situation.

Mortenson said, gloomily, “I attended the rehearsals. She was just singing the same way she always did; you know, as though she had a tail and someone was stepping on it.”

One Night of Song
— Isaac Asimov

Astro has excellent eyesight and understanding of the world around him. He is equipped with two HD cameras, and a bunch of computer vision algorithms, including facial and shape recognition. Danielle’s dream is to have him read from a music sheet and sing or play the song in a toy piano. She is very close to completing this project: Astro is able now to identify partitures, and extract from them the location of the pentagrams. Danielle is currently working on identifying the notes and the clefs. This is one of her test images, and the result of one of her early experiments:

Most of the techniques Danielle is using are accessible to any student with a decent command of vector calculus, and enough scientific maturity. The extraction of pentagrams and the different notes on them, for example, is performed with the Hough transform. This is a fancy term for an algorithm that basically searches for straight lines and circles by solving an optimization problem in two or three variables.

The only thing left is an actual performance. Danielle will be leading Fabian and Wes, and with the assistance of Mr. Simpson’s awesome students Erica and Robert, Astro will hopefully learn to physically approach the piano, choose the right keys, and play them in the correct order and speed. Talent show, anyone?

Book presentation at the USC Python Users Group

More on Lindenmayer Systems

We briefly explored Lindenmayer systems (or L-systems) in an old post: Toying with Basic Fractals. We quickly reviewed this method for creation of an approximation to fractals, and displayed an example (the Koch snowflake) based on tikz libraries.

I would like to show a few more examples of beautiful curves generated with this technique, together with their generating axiom, rules and parameters. Feel free to click on each of the images below to download a larger version.

Note that any coding language with plotting capabilities should be able to tackle this project. I used once again tikz for , but this time with the tikzlibrary lindenmayersystems.

name : Dragon Curve axiom : X order : 11 step : 5pt angle : 90 rules : X -> X+YF+ Y -> -FX-Y	name : Gosper Space-filling Curve axiom : XF order : 5 step : 2pt angle : 60 rules : XF -> XF+YF++YF-XF--XFXF-YF+ YF -> -XF+YFYF++YF+XF--XF-YF
name : Quadric Koch Island axiom : F+F+F+F order : 4 step : 1pt angle : 90 rules : F -> F+F-F-FF+F+F-F	name : Sierpinski Arrowhead axiom : F order : 8 step : 3.5pt angle : 60 rules : G -> F+G+F F -> G-F-G
name : ? axiom : F+F+F+F order : 4 step : 2pt angle : 90 rules : F -> FF+F+F+F+F+F-F	name : ? axiom : F+F+F+F order : 4 step : 3pt angle : 90 rules : F -> FF+F+F+F+FF

Would you like to experiment a little with axioms, rules and parameters, and obtain some new pleasant curves with this method? If the mathematical properties of the fractal that they approximate are interesting enough, I bet you could attach your name to them. Like the astronomer that finds through her telescope a new object in the sky, or the zoologist that discover a new species of spider in the forest.

Some results related to the Feuerbach Point

Given a triangle the circle that goes through the midpoints of each side, is called the Feuerbach circle. It has very surprising properties:

• It also goes through the feet of the heights, points
• If denotes the orthocenter of the triangle, then the Feuerbach circle also goes through the midpoints of the segments For this reason, the Feuerbach circle is also called the nine-point circle.
• The center of the Feuerbach circle is the midpoint between the orthocenter and circumcenter of the triangle.
• The area of the circumcircle is precisely four times the area of the Feuerbach circle.

Most of these results are easily shown with sympy without the need to resort to Gröbner bases or Ritt-Wu techniques. As usual, we realize that the properties are independent of rotation, translation or dilation, and so we may assume that the vertices of the triangle are and for some positive parameters To prove the last statement, for instance we may issue the following:

>>> import sympy
>>> from sympy import *
>>> A=Point(0,0)
>>> B=Point(1,0)
>>> r,s=var('r,s')
>>> C=Point(r,s)
>>> D=Segment(A,B).midpoint
>>> E=Segment(B,C).midpoint
>>> F=Segment(A,C).midpoint
>>> simplify(Triangle(A,B,C).circumcircle.area/Triangle(D,E,F).circumcircle.area)
4

But probably the most amazing property of the nine-point circle, is the fact that it is tangent to the incircle of the triangle. With exception of the case of equilateral triangles, both circles intersect only at one point: the so-called Feuerbach point.

An Automatic Geometric Proof

We are familiar with that result that states that, on any given triangle, the circumcenter, centroid and orthocenter are always collinear. I would like to illustrate how to use Gröbner bases theory to prove that the incenter also belongs in the previous line, provided the triangle is isosceles.

We start, as usual, indicating that this property is independent of shifts, rotations or dilations, and therefore we may assume that the isosceles triangle has one vertex at , another vertex at and the third vertex at for some value In that case, we will need to work on the polynomial ring since we need the parameter free, the variables and are used to input the conditions for the circumcenter of the triangle, the variables and for centroid, and the variables and for the incenter (note that we do not need to use the orthocenter in this case).

We may obtain all six conditions by using sympy, as follows:

>>> import sympy
>>> from sympy import *
>>> A=Point(0,0)
>>> B=Point(1,0)
>>> s=symbols("s",real=True,positive=True)
>>> C=Point(1/2.,s)
>>> T=Triangle(A,B,C)
>>> T.circumcenter
Point(1/2, (4*s**2 - 1)/(8*s))
>>> T.centroid
Point(1/2, s/3)
>>> T.incenter
Point(1/2, s/(sqrt(4*s**2 + 1) + 1))

This translates into the following polynomials

(for circumcenter)
(for centroid)
(for incenter)

The hypothesis polynomial comes simply from asking whether the slope of the line through two of those centers is the same as the slope of the line through another choice of two centers; we could use then, for example, It only remains to compute the Gröbner basis of the ideal Let us use SageMath for this task:

sage: R.<s,x1,x2,x3,y1,y2,y3,z>=PolynomialRing(QQ,8,order='lex')
sage: h=[2*x1-1,8*r*y1-4*r**2+1,2*x2-1,3*y2-r,2*x3-1,(4*r*y3+1)**2-4*r**2-1]
sage: g=(x2-x1)*(y3-y1)-(x3-x1)*(y2-y1)
sage: I=R.ideal(1-z*g,*h)
sage: I.groebner_basis()
[1]

This proves the result.