Jotto (5-letter Mastermind) in the NAO robot
I would like to show how to code the NAO robot to beat us at Jotto (5-letter Mastermind) with python in Choregraphe. I will employ a brute force technique that does not require any knowledge of the English language, the frequency of its letters, or smart combinations of vowels and consonants to try to minimize the number of attempts. It goes like this:
- Gather all 5-letter words with no repeated letters in a list.
- Choose a random word from that list—your guess—, and ask it to be scored ala Mastermind.
- Filter through the list all words that share the same score with your guess; discard the rest.
- Go back to step 2 and repeat until the target word is found.
Coding this strategy in python requires only four variables:
whole_dict: the list with all the wordsstep = [x for x in whole_dict]: A copy ofwhole_dict, which is going to be shortened on each step (hence the name). Note that statingstep = whole_dictwill change the contents ofwhole_dictwhen we change the contents ofstep— not a good idea.guess = random.choice(step): A random choice from the liststep.score: A string containing the two digits we obtain after scoring the guess. The first digit indicates the number of correct letters in the same position as the target word; the second digit indicates the number of correct letters in the wrong position.attempts: optional. The number of attempts at guessing words. For quality control purposes.
At this point, I urge the reader to stop reading the post and try to implement this strategy as a simple script. When done, come back to see how it can be coded in the NAO robot.
First, a screenshot of the root view in choregraph. Note the simplicity of the code.
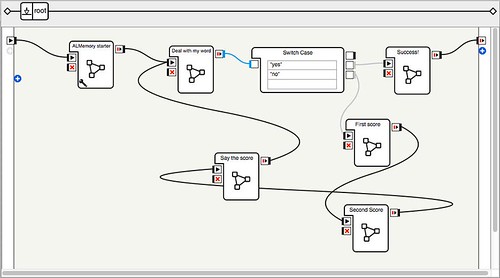
The first box, ALMemory starter, is a script box where we define all variables needed to run the program — old school. This is the code of that box:
from urllib2 import urlopen
def no_repeats(word):
""" Boolean: indicates whether a word has repeated letters """
new_word = ""
for letter in word:
if letter not in new_word:
new_word += letter
return new_word == word
# Get a list of 5-letter words from the following URL
file = urlopen("http://www.math.sc.edu/~blanco/words.txt")
words = file.read().split("\n")
file.close()
# remove words with repeated letters
words = filter(lambda x: len(x)>0, words)
words = filter(no_repeats, words)
class MyClass(GeneratedClass):
def __init__(self):
GeneratedClass.__init__(self)
pass
def onLoad(self):
# We start by creating a proxy to the memory of the robot,
# where we will insert all the needed variables
self.memoryProxy = ALProxy("ALMemory")
pass
def onUnload(self):
pass
def onInput_onStart(self):
# These are the variables we need:
self.memoryProxy.insertData("whole_dict", words)
self.memoryProxy.insertData("step", [x for x in words])
self.memoryProxy.insertData("attempts", 0)
self.memoryProxy.insertData("score", "00")
self.memoryProxy.insertData("guess", None)
self.onStopped()
pass
def onInput_onStop(self):
self.onUnload()
pass
The second box, Deal with my word, is a flow diagram containing two boxes:
- One simple script box,
Say the word. This box performs the random choice fromstep, stores it in the variableguess, and increments the value ofattemptsby one. It asks then the player ifguessis the correct word — and spells it, just in case. - A speech recognition box that expects a yes/no answer.
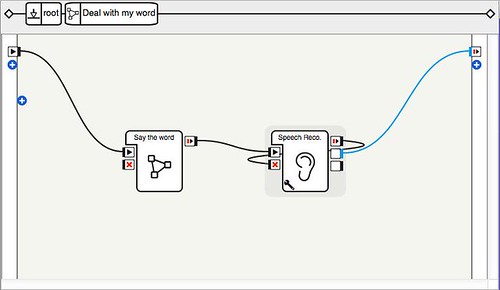
This is the code of Say the word:
from time import sleep
from random import choice
class MyClass(GeneratedClass):
def __init__(self):
GeneratedClass.__init__(self)
pass
def onLoad(self):
self.talkProxy = ALProxy("ALTextToSpeech")
self.memoryProxy = ALProxy("ALMemory")
pass
def onUnload(self):
pass
def onInput_onStart(self):
step = self.memoryProxy.getData("step")
guess = choice(step)
self.memoryProxy.insertData("guess", guess)
attempts = self.memoryProxy.getData("attempts")
self.memoryProxy.insertData("attempts", attempts + 1)
self.talkProxy.say("Is it %s?" % guess)
sleep(1)
for letter in guess:
self.talkProxy.say(letter)
sleep(1)
self.onStopped()
pass
def onInput_onStop(self):
self.onUnload()
pass
A switch case is next: if the player says “yes”, the program concludes with the script box Success!, that states the number of attempts. The code is simple, and it illustrates once again the way to access data from ALMemory. The only relevant portions of the code on that box are the methods onLoad and onInput_osStart:
def onLoad(self):
self.talkProxy = ALProxy("ALTextToSpeech")
self.memoryProxy = ALProxy("ALMemory")
pass
def onInput_onStart(self):
attempts = self.memoryProxy.getData("attempts")
self.talkProxy.say("Wonderful! I got it in %s attempts!" % str(attempts))
pass
If the player says “no”, we retrieve the two scores with two flow diagram boxes: First Score and Second Score. I will present the structure and code of the latter, and leave the code of the former as an exercise.
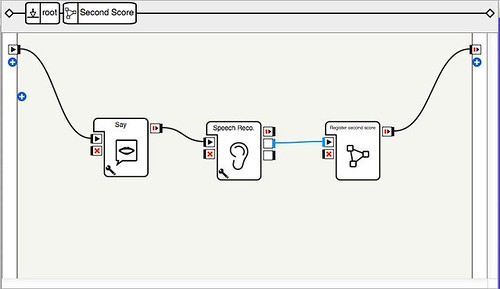
The first box is a simple Say that asks for the score. The second box is a Speech Recognition box that expects any digit from 0 to 5. The third is a script box that receives the second box output (as a string), and performs the following operation (only onLoad and onInput_onStart are shown):
def onLoad(self):
self.memoryProxy = ALProxy("ALMemory")
pass
def onInput_onStart(self, p):
score = self.memoryProxy.getData("score")
score = score[0] + p
self.memoryProxy.insertData("score", score)
self.onStopped()
pass
And finally, the script box Say the score. This is where the magic happens. In this box we receive the complete score, and filter all the words from step to eliminate those that do not share the same score as guess. We perform that with the following code:
def compute_score(guess, target):
""" This function scores guess against target,
mastermind style """
correct = 0
moved = 0
for x in range(5):
if guess[x] in target:
if guess[x] == target[x]:
correct += 1
else:
moved += 1
return str(correct)+str(moved)
def register_score(score, step, guess):
""" a simple fliter to eliminate unwanted words from step """
return filter(lambda x: compute_score(guess, x)==score, step)
class MyClass(GeneratedClass):
def __init__(self):
GeneratedClass.__init__(self)
pass
def onLoad(self):
self.memoryProxy = ALProxy("ALMemory")
self.talkProxy = ALProxy("ALTextToSpeech")
pass
def onUnload(self):
pass
def onInput_onStart(self):
score = self.memoryProxy.getData("score")
step = self.memoryProxy.getData("step")
guess = self.memoryProxy.getData("guess")
self.talkProxy.say("So, the score of %s is %s %s" % (guess, score[0], score[1]))
step = register_score(score, step, guess)
#self.talkProxy.say("We are down to %s words" % str(len(step)))
self.memoryProxy.insertData("step", step)
self.onStopped()
pass
def onInput_onStop(self):
self.onUnload()
pass
That is all! I hope you enjoy playing Jotto with your NAO. The code can be greatly improved by adding motions in the different steps, or implementing better winning strategies. With brute force, NAO is able to find your word in about 5 attempts (as average, of course). Do you think you can find a strategy that brings this number down to 4 attempts? If so, I would love to hear about it.
We have moved!
In the news:
Recent Posts
- Migration
- Computational Geometry in Python
- Searching (again!?) for the SS Central America
- Jotto (5-letter Mastermind) in the NAO robot
- Robot stories
- Advanced Problem #18
- Book presentation at the USC Python Users Group
- Areas of Mathematics
- More on Lindenmayer Systems
- Some results related to the Feuerbach Point
- An Automatic Geometric Proof
- Sympy should suffice
- A nice application of Fatou’s Lemma
- Have a child, plant a tree, write a book
- Project Euler with Julia
- Seked
- Nezumi San
- Ruthless Thieves Stealing a Roll of Cloth
- Which one is the fake?
- Stones, balances, matrices
- Buy my book!
- Trigonometry
- Naïve Bayes
- Math still not the answer
- Sometimes Math is not the answer
- What if?
- Edge detection: The Convolution Approach
- OpArt
- So you want to be an Applied Mathematician
- Smallest Groups with Two Eyes
- The ultimate metapuzzle
- Where are the powers of two?
- Geolocation
- Boundary operators
- The Cantor Pairing Function
- El País’ weekly challenge
- Math Genealogy Project
- Basic Statistics in sage
- A Homework on the Web System
- Apollonian gaskets and circle inversion fractals
- Toying with basic fractals
- Unusual dice
- Wavelets in sage
- Edge detection: The Scale Space Theory
- Bertrand Paradox
- Voronoi mosaics
- Image Processing with numpy, scipy and matplotlibs in sage
- Super-Resolution Micrograph Reconstruction by Nonlocal-Means Applied to HAADF-STEM
- The Nonlocal-means Algorithm
- The hunt for a Bellman Function.
- Presentation: Hilbert Transform Pairs of Wavelets
- Presentation: The Dual-Tree Complex Wavelet Transform
- Presentation: Curvelets and Approximation Theory
- Poster: Curvelets vs. Wavelets (Mathematical Models of Natural Images)
- Wavelet Coefficients
- Modeling the Impact of Ebola and Bushmeat Hunting on Western Lowland Gorillas
- Triangulations
- Mechanical Geometry Theorem Proving
Pages
- About me
- Books
- Curriculum Vitae
- Research
- Teaching
- Mathematical Imaging
- Introduction to the Theory of Distributions
- An Introduction to Algebraic Topology
- The Basic Practice of Statistics
- MA598R: Measure Theory
- MA122—Fall 2014
- MA141—Fall 2014
- MA142—Summer II 2012
- MA241—Spring 2014
- MA242—Fall 2013
- Past Sections
- MA122—Spring 2012
- MA122—Spring 2013
- Lesson Plan—section 007
- Lesson Plan—section 008
- Review for First part (section 007)
- Review for First part (section 008)
- Review for Second part (section 007)
- Review for Third part (section 007)
- Review for the Second part (section 008)
- Review for the Fourth part (section 007)
- Review for Third and Fourth parts (section 008)
- MA122—Fall 2013
- MA141—Spring 2010
- MA141—Fall 2012
- MA141—Spring 2013
- MA141—Fall 2013
- MA141—Spring 2014
- MA141—Summer 2014
- MA142—Fall 2011
- MA142—Spring 2012
- MA241—Fall 2011
- MA241—Fall 2012
- MA241—Spring 2013
- MA242—Fall 2012
- MA242—Spring 2012
- First Midterm Practice Test
- Second Midterm-Practice Test
- Third Midterm—Practice Test
- Review for the fourth part of the course
- Blake Rollins’ code in Java
- Ronen Rappaport’s project: messing with strings
- Sam Somani’s project: Understanding Black-Scholes
- Christina Papadimitriou’s project: Diffusion and Reaction in Catalysts
- Problem Solving
- Borsuk-Ulam and Fixed Point Theorems
- The Cantor Set
- The Jordan Curve Theorem
- My oldest plays the piano!
- How many hands did Ernie shake?
- A geometric fallacy
- What is the next number?
- Remainders
- Probability and Divisibility by 11
- Convex triangle-square polygons
- Thieves!
- Metapuzzles
- What day of the week?
- Exact Expression
- Chess puzzles
- Points on a plane
- Sequence of right triangles
- Sums of terms from Fibonacci
- Alleys
- Arithmetic Expressions
- Three circles
- Pick a point
- Bertrand Paradox
- Unusual dice
- El País’ weekly challenge
- Project Euler with Julia
- LaTeX
Categories
Archives
- November 2014
- September 2014
- August 2014
- July 2014
- June 2014
- March 2014
- December 2013
- October 2013
- September 2013
- July 2013
- June 2013
- April 2013
- January 2013
- December 2012
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- November 2011
- September 2011
- August 2011
- June 2011
- May 2011
- April 2011
- February 2011
- January 2011
- December 2010
- May 2010
- April 2010
- September 2008
- September 2007
- August 2007
 Math updates on arXiv.org
Math updates on arXiv.org
- On classical 1-absorbing prime submodules
- Addressing Unboundedness in Quadratically-Constrained Mixed-Integer Problems
- On the spectral redundancy of pineapple graphs
- Soliton resolution for the energy-critical nonlinear heat equation in the radial case
- Lipschitz regularity for Poisson equations involving measures supported on $C^{1,\operatorname{Dini}}$ interfaces
- The HLLC-2D method for the computation of two phase flow system ejecta transporting model
- Time-dependent Flows and Their Applications in Parabolic-parabolic Patlak-Keller-Segel Systems Part II: Shear Flows
- Sufficient conditions for total positivity, compounds, and Dodgson condensation
- Limit points of (singless) Laplacian spectral radii of linear trees
- Binding groups for algebraic dynamics
 sagemath
sagemath
- An error has occurred; the feed is probably down. Try again later.



